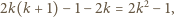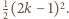Zadanie ZM-1559
o zadaniu...
- Publikacja w Delcie: marzec 2018
- Publikacja elektroniczna: 28 lutego 2018
Pierwsza ćwiartka płaszczyzny z kartezjańskim układem współrzędnych jest podzielona prostymi o równaniach 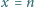 oraz
oraz 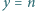 dla
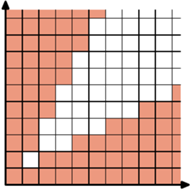
dla 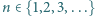 na kwadraty jednostkowe, zwane dalej polami. Czy można wyróżnić niektóre pola w taki sposób, że:
na kwadraty jednostkowe, zwane dalej polami. Czy można wyróżnić niektóre pola w taki sposób, że:
- każdy kwadrat o bokach całkowitej długości równoległych do osi układu i jednym z wierzchołków w punkcie
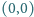 zawiera więcej pól wyróżnionych niż niewyróżnionych;
zawiera więcej pól wyróżnionych niż niewyróżnionych; - każda prosta równoległa do prostej
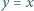 przecina wnętrze tylko skończenie wielu wyróżnionych pól?
przecina wnętrze tylko skończenie wielu wyróżnionych pól?

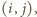 że
że 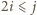 lub
lub 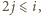 to warunki zadania będą spełnione.
to warunki zadania będą spełnione.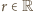 prosta
prosta 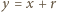 przecina skończenie wiele wyróżnionych pól, mianowicie takie pola
przecina skończenie wiele wyróżnionych pól, mianowicie takie pola 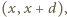 że
że ![|x∈ [0,d]∩ Z,](/math/temat/matematyka/geometria/planimetria/zadania/2018/02/28/zm-1559/4x-88b1a6d348e4abf2b8714275d417cc2bd4f3b58c-im-66,57,43-FF,FF,FF.gif) przy czym
przy czym 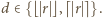
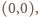 a prawym górnym
a prawym górnym 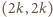 zawiera dokładnie
zawiera dokładnie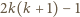
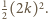 Stąd każdy kwadrat o lewym dolnym rogu
Stąd każdy kwadrat o lewym dolnym rogu 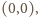 a prawym górnym
a prawym górnym 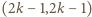 zawiera o
zawiera o 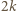 wyróżnionych pól mniej, czyli
wyróżnionych pól mniej, czyli