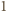Bez straty ogólności przypuśćmy, że każdy z wyjściowych trójkątów ma przeciwprostokątną długości oraz przyprostokątne długości 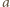oraz 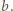Z podobieństwa trójkątów otrzymywanych podczas wykonywania cięć wynika, że każdy z otrzymywanych w wyniku cięć trójkątów będzie miał przeciwprostokątną długości 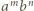dla pewnych liczb całkowitych nieujemnych 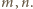Każdemu takiemu trójkątowi przyporządkujmy liczbę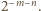

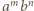Zauważmy, że dozwolone cięcie trójkąta o przeciwprostokątnej prowadzi do powstania kawałków o przeciwprostokątnych 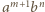oraz 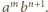Suma liczb przyporządkowanych tym trójkątom jest równa 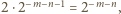czyli równa liczbie przyporządkowanej trójkątowi wyjściowemu. To oznacza, że suma liczb przyporządkowanych trójkątom nie ulega zmianie podczas wykonywania cięć.

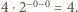Początkowo suma liczb przyporządkowanych wszystkim kawałkom papieru jest równa Gdyby w pewnym momencie żadne dwa kawałki nie były przystające, to w szczególności przyporządkowane im pary 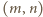byłyby różne, wobec czego suma wartości liczb przyporządkowanych wszystkim kawałkom byłaby mniejsza (ostro) od

Uzyskana sprzeczność oznacza, że w każdym momencie pewne dwa trójkąty są przystające.