Zadanie ZM-1559
o zadaniu...
- Publikacja w Delcie: grudzień 2017
- Publikacja elektroniczna: 2 grudnia 2017
Dany jest okrąg 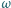 o średnicy
o średnicy 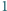 oraz łamana
oraz łamana  o końcach należących do tego okręgu, której długość jest mniejsza od
o końcach należących do tego okręgu, której długość jest mniejsza od  Udowodnić, że istnieje średnica okręgu
Udowodnić, że istnieje średnica okręgu 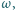 która jest rozłączna z
która jest rozłączna z 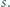

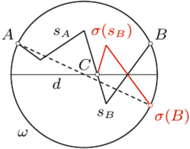
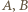 końce łamanej
końce łamanej 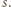 Niech
Niech 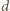 będzie średnicą okręgu
będzie średnicą okręgu 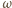 równoległą do
równoległą do 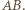 Udowodnimy, że
Udowodnimy, że 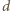 spełnia warunki zadania.
spełnia warunki zadania. ma ze średnicą
ma ze średnicą 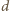 co najmniej jeden punkt wspólny
co najmniej jeden punkt wspólny 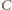 i oznaczmy fragmenty łamanej
i oznaczmy fragmenty łamanej  od punktu
od punktu 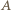 do punktu
do punktu 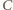 oraz od punktu
oraz od punktu 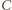 do punktu
do punktu 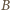 odpowiednio przez
odpowiednio przez 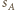 oraz
oraz 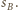
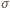 względem prostej zawierającej
względem prostej zawierającej 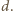 Wówczas, skoro
Wówczas, skoro 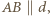 to odcinek
to odcinek 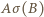 jest średnicą
jest średnicą 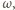 wobec czego
wobec czego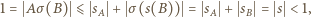
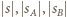 oznaczają długości odpowiednich łamanych. Uzyskana sprzeczność kończy rozwiązanie zadania.
oznaczają długości odpowiednich łamanych. Uzyskana sprzeczność kończy rozwiązanie zadania.