Środek przeciwprostokątnej»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Środek przeciwprostokątnej
- Publikacja w Delcie: sierpień 2017
- Publikacja elektroniczna: 30 lipca 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (99 KB)
Proste 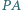 i
i 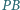 są styczne do okręgu
są styczne do okręgu 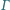 odpowiednio w punktach
odpowiednio w punktach 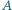 i
i 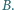 Punkt
Punkt 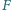 jest rzutem prostokątnym punktu
jest rzutem prostokątnym punktu 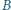 na średnicę
na średnicę 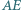 okręgu
okręgu 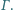 Wykaż, że środek odcinka
Wykaż, że środek odcinka 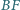 leży na prostej
leży na prostej 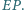


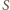 punkt przecięcia prostych
punkt przecięcia prostych 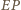 i
i 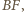 a przez
a przez 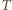 - punkt przecięcia prostych
- punkt przecięcia prostych 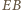 i
i 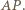 Obydwie proste
Obydwie proste 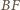 i
i 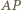 są prostopadłe do
są prostopadłe do 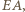 więc trójkąty
więc trójkąty 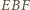 oraz
oraz 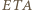 są podobne i
są podobne i 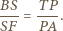
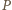 jest środkiem odcinka
jest środkiem odcinka 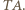
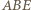 jest prosty (gdyż
jest prosty (gdyż 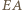 jest średnicą okręgu), stąd także kąt
jest średnicą okręgu), stąd także kąt 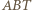 jest prosty. Odcinki
jest prosty. Odcinki 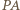 i
i 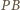 są równe jako styczne do okręgu. Wobec tego punkt
są równe jako styczne do okręgu. Wobec tego punkt 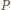 leży na przeciwprostokątnej trójkąta prostokątnego
leży na przeciwprostokątnej trójkąta prostokątnego 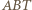 i zarazem na symetralnej jednej z przyprostokątnych, jest więc środkiem okręgu opisanego na tym trójkącie, czyli także środkiem boku
i zarazem na symetralnej jednej z przyprostokątnych, jest więc środkiem okręgu opisanego na tym trójkącie, czyli także środkiem boku 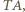 co kończy dowód.
co kończy dowód.