Zadanie ZM-1535
o zadaniu...
- Publikacja w Delcie: lipiec 2017
- Publikacja elektroniczna: 30 czerwca 2017
Czy na płaszczyźnie można wskazać taki niezawarty w prostej, co najmniej
trzyelementowy, zbiór punktów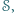 
że dla każdych trzech niewspółliniowych punktów 
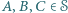środek okręgu opisanego na trójkącie 
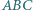również należy do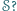 
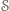istnieje. Spośród wszystkich odcinków o obu końcach w zbiorze 
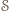wybierzmy taki, który ma najmniejszą długość i nazwijmy go 
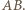Ponieważ zbiór 
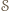nie jest zawarty w prostej, więc poza prostą 
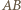jest co najmniej jeden punkt zbioru 
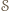- spośród wszystkich takich punktów wybierzmy taki punkt 
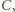dla którego miara kąta 
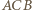jest największa.
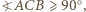to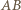 
jest najdłuższym bokiem trójkąta 
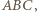co przeczy wyborowi odcinka 
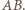Z kolei jeżeli 
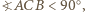to środek 
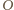okręgu opisanego na trójkącie 
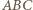należy do 
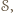przy czym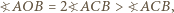
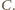Uzyskana sprzeczność oznacza, że nie istnieje zbiór 
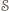o zadanych własnościach.