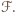Zadanie ZM-1530
o zadaniu...
- Publikacja w Delcie: maj 2017
- Publikacja elektroniczna: 1 maja 2017
Na okręgu o długości 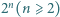 znajdują się punkty
znajdują się punkty 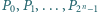 będące wierzchołkami
będące wierzchołkami 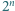 -kąta foremnego, oznaczone w taki sposób, że długość łuku
-kąta foremnego, oznaczone w taki sposób, że długość łuku 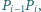 mierzonego zgodnie z ruchem wskazówek zegara, jest równa
mierzonego zgodnie z ruchem wskazówek zegara, jest równa 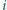 dla każdego
dla każdego 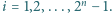 Niech
Niech

Udowodnić, że 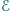 i
i 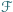 są przystające (jako podzbiory płaszczyzny).
są przystające (jako podzbiory płaszczyzny).

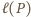 będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego
będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego 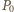 z
z 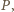 tzn. dla każdego
tzn. dla każdego 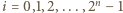
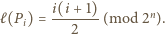
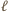 jest bijekcją zbioru wierzchołków
jest bijekcją zbioru wierzchołków 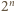 -kąta i
-kąta i ![|Z ∩ [0,2n −1].](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/30/zm-1530/8x-5a02d8212f68e6296da2e894dc2a3a250bf72f4c-im-66,57,43-FF,FF,FF.gif)
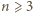 zachodzi równość
zachodzi równość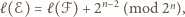
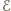 jest obrazem
jest obrazem 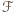 przy obrocie o
przy obrocie o 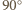 wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego
wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego 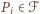
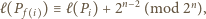
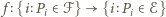 określona jest następująco
określona jest następująco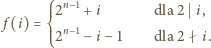
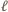 wystarczy więc sprawdzić, że dla każdego
wystarczy więc sprawdzić, że dla każdego 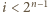 liczba
liczba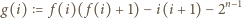
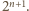 Rzeczywiście, bezpośrednio z definicji funkcji
Rzeczywiście, bezpośrednio z definicji funkcji 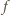 otrzymujemy, że jeżeli
otrzymujemy, że jeżeli 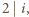 to
to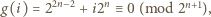
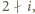 to
to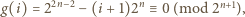
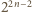 dzieli się przez
dzieli się przez 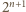 dla
dla 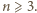 Pozostaje bezpośrednio sprawdzić, że dla
Pozostaje bezpośrednio sprawdzić, że dla 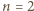 rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o
rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o 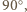 ale w przeciwną stronę).
ale w przeciwną stronę).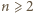 istnieje etykietowanie wierzchołków
istnieje etykietowanie wierzchołków 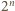 -kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie
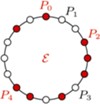
-kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie 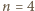 z zaznaczonymi zbiorami
z zaznaczonymi zbiorami 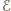 oraz
oraz