Zadanie ZM-1500
o zadaniu...
- Publikacja w Delcie: lipiec 2016
- Publikacja elektroniczna: 1 lipca 2016
Boki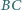 
i 
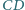prostokąta 
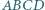są styczne odpowiednio w punktach 
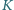i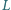 
do okręgu przechodzącego przez 
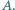Na odcinku 
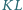leży taki punkt 
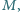że proste 
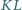i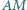 
są prostopadłe. Obliczyć pole prostokąta 
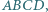wiedząc, że odcinek 
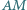ma długość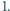 
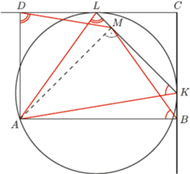
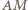jest prostopadła do 
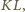więc jest nachylona do boków prostokąta pod kątem 
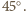Ponadto kąt środkowy oparty na cięciwie 
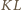jest prosty, a stąd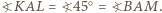 
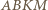jest opisany na okręgu o średnicy 
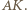W takim razie kąty 
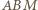i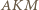 
są równe.
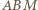i 
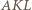są podobne. Analogicznie trójkąty 
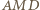i 
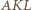są podobne. W takim razie mamy podobieństwo trójkątów 
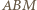i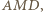 
a stąd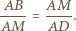
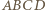jest równe 