Zadanie ZM-1494
o zadaniu...
- Publikacja w Delcie: maj 2016
- Publikacja elektroniczna: 1 maja 2016
Przekątne czworokąta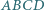 
wpisanego w okrąg o środku 
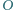przecinają się w punkcie 
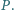Niech 
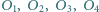będą środkami okręgów opisanych odpowiednio na trójkątach 
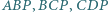i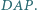 
Wykazać, że proste 
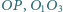i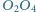 
przecinają się w jednym punkcie.
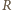będzie punktem przecięcia prostej 
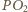z prost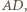ą 
a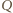 
różnym od 
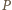punktem przecięcia tej prostej z okręgiem opisanym na trójkącie 
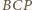(rysunek). Wówczas 
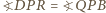oraz
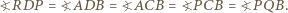
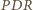i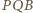 
są podobne, w szczególności 
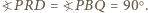Stąd prosta 
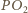jest prostopadła do 
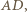a więc również równoległa do 
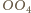- symetralnej 
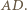Analogicznie proste 
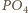i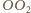 
są równoległe. W takim razie odcink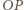i 
i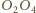 
przecinają się w połowie jako przekątne równoległoboku.
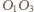przechodzi przez środek odcinka 
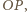co daje tezę.