Mały wybór? I dobrze!»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: 46 Olimpiada Matematyczna
- Zadanie pochodzi z artykułu Mały wybór? I dobrze!
- Publikacja w Delcie: listopad 2015
- Publikacja elektroniczna: 01-11-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (96 KB)
Dany jest taki czworokąt wypukły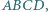 
że 
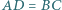oraz bok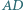i 
i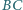 
nie są równoległe. Zmienne punkty 
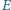i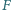 
należą odpowiednio do boków 
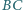i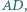 
przy czym 
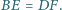Proste 
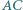i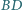 
przecinają się w punkcie 
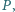proste 
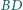i 
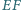w punkcie 
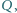a proste 
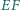i 
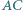- w punkcie 
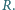Wykaż, że okręgi opisane na trójkątach 
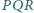mają wspólny punkt różny od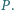 
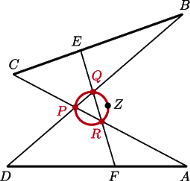
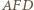na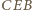 
; oznaczmy jego środek przez 
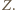Podobnie jak w rozwiązaniu zadania 3, punkt 
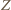należy do symetralnych odcinków 
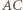i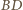 
(a więc nie zależy od wyboru punktów 
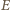i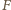 
) oraz do symetralnej 
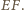Stąd rzutami punktu 
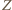na odcinki 
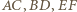są ich środki.
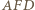na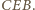 
Na mocy (*), środki odcinków 
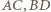i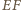 
są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu 
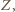więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt 
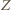leży na każdym z okręgów opisanych na zmiennych trójkątach 