Mały wybór? I dobrze!»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Mały wybór? I dobrze!
- Publikacja w Delcie: listopad 2015
- Publikacja elektroniczna: 01-11-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (96 KB)
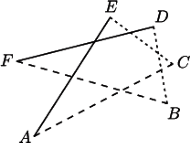
W sześciokącie wypukłym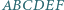 
zachodzą równości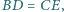 
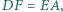
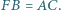Wykaż, że symetralne boków 
przecinają się w jednym punkcie.
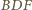i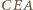 
są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcink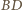i 
i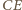 
przecinają się, jako przekątne czworokąta wypukłego 
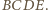Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez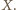 
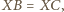czyli punkt 
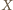leży na symetralnej odcinka 
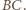Analogicznie leży też na symetralnych 
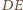i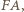 
co kończy dowód.