Prosta Simsona»Zadanie 5
o zadaniu...
- Zadanie olimpijskie: XII OM
- Zadanie pochodzi z artykułu Prosta Simsona
- Publikacja w Delcie: październik 2015
- Publikacja elektroniczna: 30-09-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (81 KB)
Cztery proste przecinające sią w sześciu punktach tworzą cztery trójkąty. Udowodnij, że okręgi opisane na tych trójkątach mają punkt wspólny.
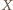będzie punktem przecięcia dwóch z danych prostych. Pozostałe dwie proste nie są równoległe, stąd dwa trójkąty o wierzchołku 
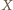nie są jednokładne, więc opisane na nich okręgi nie są styczne w 
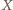i mają drugi punkt wspólny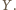 
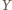na wszystkie dane proste są współliniowe. Znów na mocy tego twierdzenia, punkt 
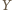należy wówczas także do pozostałych dwóch z danych okręgów.