Prosta Simsona»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Prosta Simsona
- Publikacja w Delcie: październik 2015
- Publikacja elektroniczna: 30-09-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (81 KB)
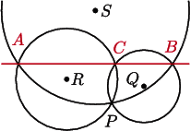
Trzy okręgi mają wspólny punkt, a pozostałe trzy punkty ich przecięć są współliniowe. Wykaż, że środki okręgów oraz ich wspólny punkt leżą na jednym okręgu.
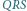
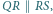
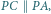
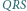
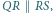
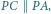
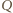i 
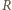leżą na symetralnej odcinka 
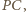więc rzutem punktu 
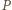na prostą 
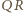jest środek 
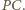Podobnie dla 
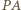i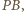 
więc rzuty 
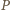na proste zawierające boki trójkąta 
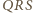leżą na jednej prostej (równoległej do 
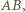dwukrotnie bliżej punktu 
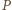) i teza wynika z twierdzenia o prostej Simsona.