Zabawy w kącie»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Zabawy w kącie
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (130 KB)
Przez dany punkt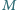 
leżący we wnętrzu kąta o wierzchołku 
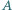poprowadzić prostą, która, przecinając ramiona kąta w punktach 
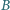i 
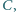wyznacza trójkąt 
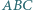o najmniejszym obwodzie.
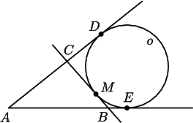
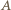wpisujemy dwa okręgi przechodzące przez punkt 
(
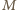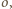w punkcie 
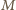wyznaczamy styczną, która przecina ramiona kąta w punktach 
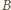i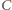 
(
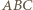spełnia warunki zadania i ma najmniejszy obwód równy 
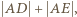gdzie 
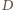i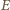 
to punkty styczności okręgu 
z ramionami kąta (jest tak, bo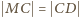 
i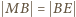 
).
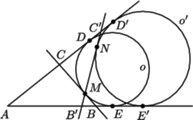
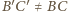jest inną prostą zawierającą punkt 
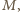to okrąg 
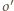dopisany do trójkąta 
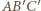jest styczny do ramion kąta w punktach 
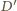i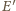 
oraz do odcinka 
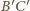w punkcie 
(
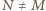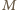leży na zewnątrz okręgu dopisanego 
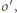więc okrąg 
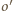ma większy promień niż okrąg 
i obwód trójkąta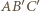 
jest równy 