Odp. Nie!
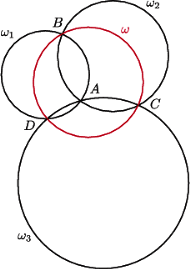
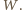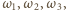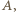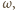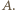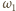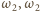Przypuśćmy, że istnieje taki zbiór Wówczas istnieją w tym zbiorze okręgi które mają punkt wspólny oraz okrąg który nie przechodzi przez Oznaczmy punkty wspólne, różne od okręgów i 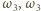i i 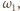odpowiednio prze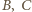z oraz 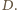Wówczas 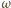przechodzi przez wszystkie te punkty.

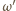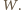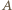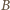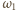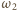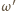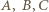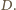Rozważmy piąty okrąg ze zbioru Musi on przechodzić przez lub (ponieważ są to jedyne punkty wspólne okręgów i ). Podobnie okrąg musi przechodzić przez co najmniej jeden z każdej pary punktów spośród i Stąd 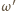przechodzi przez co najmniej trzy z tych punktów. To jest jednak niemożliwe, bo każda taka trójka wyznacza jednoznacznie jeden z okręgów