Zadanie ZM-1462
o zadaniu...
- Publikacja w Delcie: lipiec 2015
- Publikacja elektroniczna: 30-06-2015
Na płaszczyźnie dany jest zbiór punktów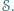 
Mówimy, że punkt 
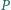jest widoczny z punktu 
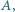jeśli odcinek 
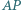jest zawarty w 
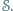Zbiór 
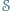jest widoczny z punktu 
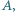jeśli każdy jego punkt jest widoczny z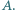 
Wykazać, że zbiór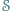 
jest widoczny z każdego punktu trójkąta 
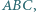jeśli jest widoczny z każdego wierzchołka tego trójkąta.
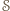jest widoczny z 
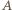i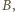 
to jest widoczny z każdego punktu odcinka 
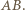To wystarczy, bowiem dowolny punkt 
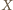z trójkąta 
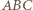leży na pewnym odcinku 
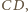dla pewnego 
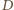z odcinka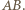 
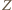na odcinku 
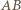i weźmy dowolny punkt 
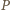z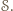 
Chcemy wykazać, że odcinek 
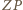leży w 
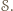Niech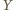 
będzie dowolnym punktem na odcinku 
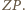Ponieważ 
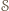widać z 
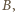to każdy punkt odcinka 
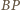leży w 
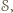w szczególności 
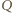- punkt przecięcia odcinka 
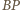z prostą 
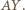Ponieważ 
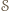widać też z 
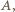to każdy punkt odcinka 
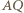należy do 
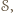w szczególności punkt 