Klub 44M - zadania XII 2014»Zadanie 692
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XII 2014
- Publikacja w Delcie: grudzień 2014
- Publikacja elektroniczna: 1 grudnia 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (59 KB)
-
Zadanie 692 zaproponował pan Adam Dzedzej z Gdańska.
Dany jest trójkąt 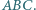 Rozważamy trzy elipsy: każda z nich ma ogniska w dwóch wierzchołkach tego trójkąta i przechodzi przez trzeci wierzchołek. Pokazać, że te trzy elipsy mają punkt wspólny wtedy i tylko wtedy, gdy trójkąt
Rozważamy trzy elipsy: każda z nich ma ogniska w dwóch wierzchołkach tego trójkąta i przechodzi przez trzeci wierzchołek. Pokazać, że te trzy elipsy mają punkt wspólny wtedy i tylko wtedy, gdy trójkąt 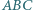 jest prostokątny.
jest prostokątny.

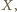 leżący w odległościach
leżący w odległościach 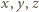 odpowiednio od wierzchołków
odpowiednio od wierzchołków 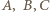 zadanego trójkąta, o bokach długości
zadanego trójkąta, o bokach długości 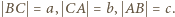 Elipsa o ogniskach
Elipsa o ogniskach 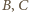 przechodzi przez punkty
przechodzi przez punkty 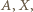 więc
więc 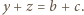 Analogicznie
Analogicznie 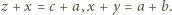 Ten układ równań z niewiadomymi
Ten układ równań z niewiadomymi 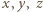 ma jedyne rozwiązanie
ma jedyne rozwiązanie 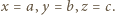 Odległości punktu
Odległości punktu 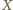 od
od 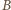 oraz
oraz 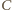 wynoszą więc, odpowiednio,
wynoszą więc, odpowiednio, 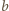 oraz
oraz  - czyli przeciwnie niż odległości punktu
- czyli przeciwnie niż odległości punktu 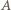 od
od 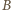 oraz
oraz 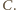 To wyznacza dwa możliwe położenia punktu
To wyznacza dwa możliwe położenia punktu 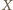 - może to być punkt symetryczny do
- może to być punkt symetryczny do 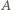 względem symetralnej odcinka
względem symetralnej odcinka 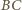 lub punkt symetryczny do
lub punkt symetryczny do 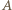 względem środka odcinka
względem środka odcinka 
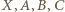 są wierzchołkami trapezu równoramiennego
są wierzchołkami trapezu równoramiennego 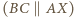 ; w drugim - tworzą równoległobok
; w drugim - tworzą równoległobok 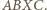 Dodatkowa informacja, że
Dodatkowa informacja, że 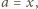 czyli
czyli 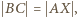 daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt
daje w obu przypadkach wniosek, że ów czworokąt jest prostokątem. A zatem trójkąt 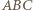 jest prostokątny.
jest prostokątny.