Teoria czy praktyka?»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Teoria czy praktyka?
- Publikacja w Delcie: listopad 2013
- Publikacja elektroniczna: 01-11-2013
Przeciwległe krawędzie czworościanu mają długości odpowiednio
 i
i
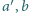 i
i
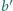 oraz
oraz
 i
i
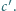 Wykaż, że
z odcinków o długościach
Wykaż, że
z odcinków o długościach
 można zbudować
trójkąt.
można zbudować
trójkąt.


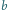
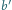

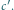
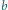
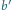

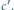
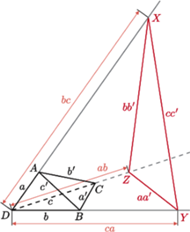
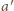 danego czworościanu
i zawierające ją ściany. Obróćmy wokół niej jedną z tych ścian tak, aby
znalazła się w tej samej płaszczyźnie, co druga, ale po przeciwnej stronie tej
krawędzi.
danego czworościanu
i zawierające ją ściany. Obróćmy wokół niej jedną z tych ścian tak, aby
znalazła się w tej samej płaszczyźnie, co druga, ale po przeciwnej stronie tej
krawędzi.
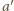 ; oznaczmy drugą przez
; oznaczmy drugą przez
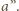 W wyjściowym czworościanie odcinek
W wyjściowym czworościanie odcinek
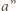 odpowiada
łamanej łączącej końce krawędzi
odpowiada
łamanej łączącej końce krawędzi
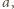 więc z nierówności trójkąta
więc z nierówności trójkąta
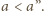
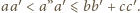 Analogicznie
dowodzimy pozostałych dwóch nierówności trójkąta dla odcinków
o długościach
Analogicznie
dowodzimy pozostałych dwóch nierówności trójkąta dla odcinków
o długościach
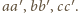
 ; z uwagi
na przemienność iloczynów
; z uwagi
na przemienność iloczynów
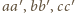 możemy przyjąć,
że
możemy przyjąć,
że
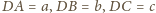 (
(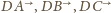 wybierzmy takie punkty odpowiednio
wybierzmy takie punkty odpowiednio
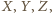 aby
aby
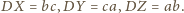 Punkty
Punkty
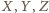 nie są współliniowe,
ponieważ rozważane półproste nie leżą w jednej płaszczyźnie.
nie są współliniowe,
ponieważ rozważane półproste nie leżą w jednej płaszczyźnie.
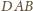 i
i
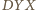 są podobne, bo mają wspólny kąt przy
wierzchołku
są podobne, bo mają wspólny kąt przy
wierzchołku
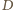 oraz
oraz
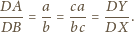
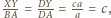 czyli
czyli
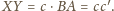
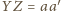 oraz
oraz
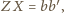 więc
trójkąt
więc
trójkąt
 ma boki o żądanych długościach.
ma boki o żądanych długościach.