Identyczne rysunki»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Identyczne rysunki
- Publikacja w Delcie: sierpień 2013
- Publikacja elektroniczna: 31-07-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Dany jest trójkąt równoramienny
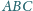 o podstawie
o podstawie
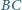 i okrąg
i okrąg
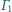 opisany na tym trójkącie. Okrąg
opisany na tym trójkącie. Okrąg
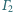 jest styczny do prostej
jest styczny do prostej
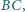 ale nie do odcinka
ale nie do odcinka
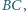 oraz do tego łuku
oraz do tego łuku
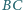 okręgu
okręgu
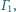 do którego należy punkt
do którego należy punkt
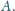 Prosta
Prosta
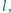 przechodząca przez
punkt
przechodząca przez
punkt
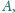 jest styczna do okręgu
jest styczna do okręgu
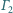 w punkcie
w punkcie
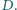 Wykaż,
że
Wykaż,
że
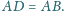


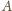 i promieniu
i promieniu
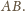 Obrazem okręgu
Obrazem okręgu
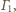 przechodzącego przez środek inwersji
przechodzącego przez środek inwersji
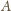 oraz przez punkty
oraz przez punkty
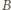 i
i
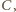 jest prosta przez punkty
jest prosta przez punkty
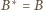 i
i
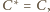 czyli prosta
czyli prosta
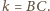 Stąd też
Stąd też
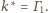
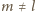 będzie prostą przechodzącą przez punkt
będzie prostą przechodzącą przez punkt
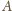 i styczną
do
i styczną
do
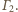 Obrazem okręgu
Obrazem okręgu
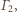 nieprzechodzącego przez środek
inwersji, jest okrąg styczny do
nieprzechodzącego przez środek
inwersji, jest okrąg styczny do
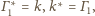
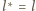 oraz
oraz
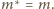 Jedynym takim okręgiem jest
Jedynym takim okręgiem jest
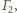 stąd
stąd
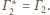
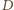 to punkt styczności prostej
to punkt styczności prostej
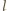 i okręgu
i okręgu
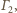 więc
jego obrazem jest punkt styczności
więc
jego obrazem jest punkt styczności
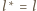 oraz
oraz
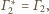 czyli on
sam:
czyli on
sam:
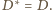 Wobec tego z warunku
Wobec tego z warunku
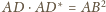 wynika, że
wynika, że
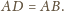
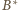 zamiast
zamiast