Identyczne rysunki»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Identyczne rysunki
- Publikacja w Delcie: sierpień 2013
- Publikacja elektroniczna: 31-07-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Okręgi
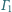 i
i
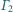 są rozłączne zewnętrznie, a ich wspólne
styczne zewnętrzne przecinają się w punkcie
są rozłączne zewnętrznie, a ich wspólne
styczne zewnętrzne przecinają się w punkcie
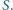 Okrąg
Okrąg
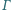 jest
styczny zewnętrznie do okręgów
jest
styczny zewnętrznie do okręgów
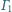 i
i
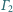 odpowiednio
w punktach
odpowiednio
w punktach
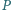 i
i
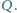 Wykaż, że punkty
Wykaż, że punkty
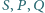 są
współliniowe.
są
współliniowe.


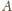 i
i
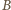 będą punktami styczności okręgów odpowiednio
będą punktami styczności okręgów odpowiednio
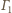 i
i
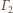 do jednej z danych prostych. Rozważmy inwersję
względem okręgu o środku
do jednej z danych prostych. Rozważmy inwersję
względem okręgu o środku
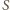 i promieniu
i promieniu
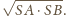 Obie
rozpatrywane proste styczne są stałe, bo przechodzą przez środek inwersji
Obie
rozpatrywane proste styczne są stałe, bo przechodzą przez środek inwersji
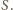 Punkt
Punkt
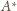 leży na półprostej
leży na półprostej
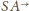 i spełnia warunek
i spełnia warunek
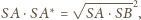 stąd
stąd
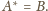 Obrazem okręgu
Obrazem okręgu
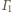 jest
okrąg (bo
jest
okrąg (bo
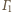 nie przechodzi przez punkt
nie przechodzi przez punkt
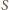 ), styczny do danych
prostych (bo są one stałe) i przechodzący przez punkt
), styczny do danych
prostych (bo są one stałe) i przechodzący przez punkt
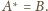 Wobec tego
Wobec tego
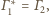 stąd także
stąd także
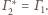
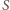 leży na zewnątrz okręgu
leży na zewnątrz okręgu
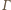 ; niech
; niech
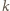 i
i
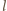 będą
prostymi stycznymi do
będą
prostymi stycznymi do
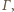 poprowadzonymi z
poprowadzonymi z
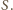 Obrazem
Obrazem
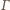 jest okrąg styczny do
jest okrąg styczny do
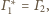
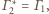
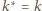 oraz
oraz
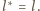 Jedynym takim okręgiem jest właśnie
Jedynym takim okręgiem jest właśnie
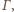 czyli
czyli
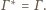
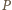 to punkt styczności
to punkt styczności
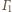 i
i
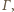 więc jego obrazem jest
punkt styczności
więc jego obrazem jest
punkt styczności
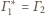 i
i
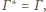 czyli
czyli
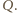 Środek
inwersji
Środek
inwersji
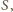 punkt
punkt
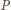 i jego obraz
i jego obraz
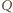 są współliniowe.
są współliniowe.
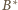 zamiast
zamiast