Zadanie ZM-1366
o zadaniu...
- Publikacja w Delcie: listopad 2012
- Publikacja elektroniczna: 01-11-2012
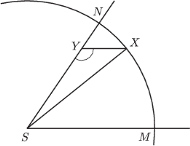
Dany jest kąt ostry
 przy czym
przy czym
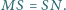 Punkt
Punkt
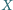 leży na krótszym łuku
leży na krótszym łuku
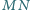 okręgu o środku
okręgu o środku
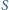 i promieniu
i promieniu
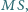 punkt
punkt
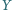 jest takim punktem odcinka
jest takim punktem odcinka
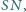 że proste
że proste
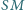 i
i
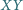 są równoległe. Znaleźć takie
położenie punktu
są równoległe. Znaleźć takie
położenie punktu
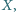 przy którym pole trójkąta
przy którym pole trójkąta
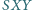 jest
największe.
jest
największe.

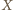 jest środkiem łuku
jest środkiem łuku
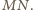
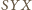 ma stałą miarę (niezależną od wyboru punktu
ma stałą miarę (niezależną od wyboru punktu
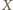 ),
a odcinek
),
a odcinek
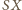 – stałą długość. Wszystkie rozważane trójkąty
– stałą długość. Wszystkie rozważane trójkąty
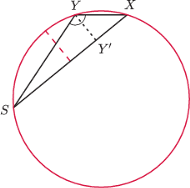
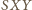 można więc wpisać w ten sam okrąg, przy czym kąt
można więc wpisać w ten sam okrąg, przy czym kąt
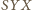 jest oparty na ustalonej cięciwie. Pole takiego trójkąta wynosi
jest oparty na ustalonej cięciwie. Pole takiego trójkąta wynosi
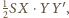 gdzie
gdzie
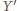 to rzut prostokątny punktu
to rzut prostokątny punktu
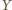 na
na
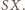 Jest ono największe, gdy
Jest ono największe, gdy
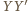 jest największe, czyli wtedy
i tylko wtedy, gdy
jest największe, czyli wtedy
i tylko wtedy, gdy
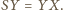 Ale to jest równoważne temu, że
Ale to jest równoważne temu, że
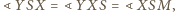 czyli temu, że
czyli temu, że
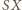 jest dwusieczną
kąta
jest dwusieczną
kąta