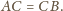Zadanie ZM-1364
o zadaniu...
- Publikacja w Delcie: październik 2012
- Publikacja elektroniczna: 30-09-2012
Znaleźć wszystkie trójkąty ostrokątne
 wpisane w ustalony
okrąg
wpisane w ustalony
okrąg
 spełniające następujący warunek: środek ciężkości
spełniające następujący warunek: środek ciężkości
 trójkąta
trójkąta
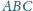 pokrywa się z ortocentrum
pokrywa się z ortocentrum
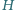 trójkąta
trójkąta
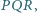 gdzie
gdzie
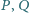 i
i
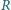 to odpowiednio punkty przecięcia
półprostych
to odpowiednio punkty przecięcia
półprostych
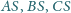 z okręgiem
z okręgiem
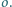


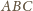 musi być równoboczny.
musi być równoboczny.
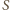 jest ortocentrum trójkąta
jest ortocentrum trójkąta
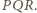 Mamy
równość kątów
Mamy
równość kątów
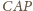 i
i
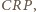 jako wpisanych opartych na tym
samym łuku. Skoro jednak
jako wpisanych opartych na tym
samym łuku. Skoro jednak
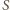 jest ortocentrum, to kąt
jest ortocentrum, to kąt
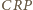 jest
równy kątowi
jest
równy kątowi
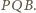 Ten z kolei jest oparty na tym samym łuku co kąt
Ten z kolei jest oparty na tym samym łuku co kąt
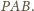 Zatem
Zatem
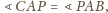 czyli
czyli
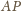 jest dwusieczną
i zarazem środkową w trójkącie
jest dwusieczną
i zarazem środkową w trójkącie
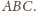 Zatem
Zatem
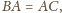 co
wynika np. z twierdzenia o dwusiecznej. Analogicznie dowodzimy, że
co
wynika np. z twierdzenia o dwusiecznej. Analogicznie dowodzimy, że