Zadanie ZM-1354
o zadaniu...
- Publikacja w Delcie: lipiec 2012
- Publikacja elektroniczna: 01-07-2012

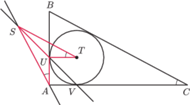
Dany jest nierównoramienny trójkąt prostokątny
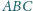 o kącie
prostym przy wierzchołku
o kącie
prostym przy wierzchołku
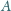 . Niech
. Niech
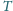 będzie środkiem
okręgu wpisanego, zaś
będzie środkiem
okręgu wpisanego, zaś
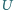 i
i
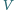 niech będą jego punktami
styczności odpowiednio z bokami
niech będą jego punktami
styczności odpowiednio z bokami
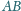 i
i
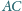 . Prosta
. Prosta
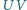 przecina w punkcie
przecina w punkcie
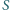 styczną do okręgu opisanego poprowadzoną
w punkcie
styczną do okręgu opisanego poprowadzoną
w punkcie
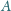 . Udowodnić, że proste
. Udowodnić, że proste
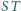 i
i
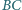 są równoległe.
są równoległe.

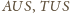 są przystające
na mocy cechy bkb (oczywiście
są przystające
na mocy cechy bkb (oczywiście
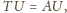 a ponadto
a ponadto
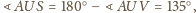
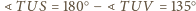 ).
).
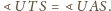 Natomiast z twierdzenia o stycznej do
okręgu i kącie wpisanym, zastosowanego do okręgu opisanego na trójkącie
Natomiast z twierdzenia o stycznej do
okręgu i kącie wpisanym, zastosowanego do okręgu opisanego na trójkącie
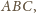 mamy
mamy
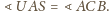 Wobec tego kąty
Wobec tego kąty
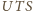 i
i
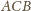 są równe, co kończy dowód.
są równe, co kończy dowód.