Konferencja w Ameliówce»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Konferencja w Ameliówce
- Publikacja w Delcie: marzec 2012
- Publikacja elektroniczna: 02-03-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (71 KB)
Niech
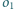 i
i
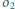 będą rozłącznymi okręgami, takimi że
będą rozłącznymi okręgami, takimi że
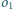 leży we wnętrzu
leży we wnętrzu
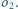 Rysujemy okrąg
Rysujemy okrąg
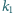 styczny
zewnętrznie do
styczny
zewnętrznie do
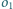 i wewnętrznie do
i wewnętrznie do
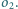 Następnie rysujemy okrąg
Następnie rysujemy okrąg
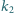 styczny zewnętrznie do
styczny zewnętrznie do
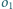 i
i
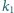 oraz wewnętrznie do
oraz wewnętrznie do
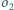 itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
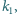 to mówimy, że okręgi
to mówimy, że okręgi
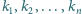 tworzą
łańcuch Steinera okręgów
tworzą
łańcuch Steinera okręgów
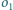 i
i
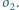 Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
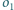 i
i
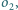 to jest to niezależne od
położenia pierwszego okręgu
to jest to niezależne od
położenia pierwszego okręgu