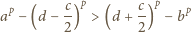Klub 44M - zadania XI 2011»Zadanie 630
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2011
- Publikacja w Delcie: listopad 2011
- Publikacja elektroniczna: 01-11-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (62 KB)
Zadanie zaproponował pan Tomasz Tkocz z Warszawy.
W trójkącie ostrokątnym o bokach długości
środkowa
poprowadzona do boku
ma długość
Wykazać, że dla
każdej liczby dodatniej
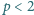zachodzi nierówność
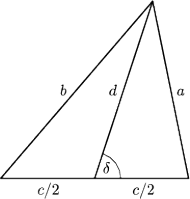
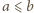i oznaczmy przez
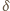miarę kąta ostrego (lub
prostego), jaki zadana środkowa tworzy z prostą, zawierającą bok
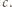Jest to
kąt wewnętrzny w trójkącie o bokach długości
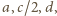przeciwległy
bokowi
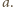Ze wzoru kosinusów:
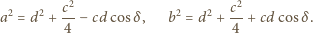
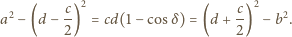
jest funkcją ściśle wklęsłą (w pewnym przedziale)
i jeśli
jest stałą dodatnią, to funkcja
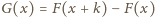jest
ściśle malejąca. Zastosujmy tę własność do funkcji
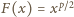(ściśle
wklęsłej w przedziale
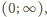skoro
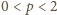) oraz do
stałej dodatniej
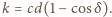Tworzymy funkcję malejącą
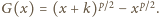
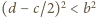(równoważnie:
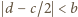; jest
to nierówność dla boków jednego z trójkątów, na które środkowa
dzieli trójkąt wyjściowy). Zatem
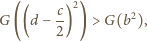
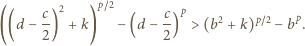
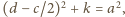
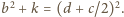Otrzymujemy
nierówność
