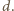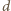W przestrzeni łatwiej!»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu W przestrzeni łatwiej!
- Publikacja w Delcie: wrzesień 2011
- Publikacja elektroniczna: 31-08-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (58 KB)
32 proste dzielą koło o promieniu 10 cm na pewną liczbę części. Udowodnij, że w jednej z nich da się zmieścić okrągły guzik o promieniu 3 mm.


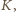 współśrodkowe z nim, o promieniu 97 mm. Czy jest możliwe, aby
kolorowe pasy pokryły całe koło
współśrodkowe z nim, o promieniu 97 mm. Czy jest możliwe, aby
kolorowe pasy pokryły całe koło
 ? Jeśli nie, to dowolny z niepokrytych
punktów „nadaje się” jako środek guzika. Jak oszacować pole powierzchni
koła przykrytej przez pasy?
? Jeśli nie, to dowolny z niepokrytych
punktów „nadaje się” jako środek guzika. Jak oszacować pole powierzchni
koła przykrytej przez pasy?

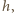
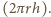
 z pasami
jako na rzut (widok z góry) pewnej kuli, wtedy pasy te odpowiadają
plastrom. Wobec tego łączne pole 32 pasów na powierzchni kuli równe
jest co najwyżej
z pasami
jako na rzut (widok z góry) pewnej kuli, wtedy pasy te odpowiadają
plastrom. Wobec tego łączne pole 32 pasów na powierzchni kuli równe
jest co najwyżej
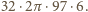 Tymczasem powierzchnia kuli
o promieniu 97 mm równa jest
Tymczasem powierzchnia kuli
o promieniu 97 mm równa jest
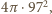 czyli więcej. Zatem
pasy nie pokrywają całej kuli, więc ich rzuty nie pokrywają całego koła
czyli więcej. Zatem
pasy nie pokrywają całej kuli, więc ich rzuty nie pokrywają całego koła
 i w dowolnym z niepokrytych punktów możemy umieścić
środek guzika o promieniu 3 mm.
i w dowolnym z niepokrytych punktów możemy umieścić
środek guzika o promieniu 3 mm.
 o promieniu 97 mm. Dowiedliśmy, że żadne
inne ich ułożenie też nie wystarcza. W 1932 r. A. Tarski postawił
ogólniejszy
o promieniu 97 mm. Dowiedliśmy, że żadne
inne ich ułożenie też nie wystarcza. W 1932 r. A. Tarski postawił
ogólniejszy