W przestrzeni łatwiej!»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu W przestrzeni łatwiej!
- Publikacja w Delcie: wrzesień 2011
- Publikacja elektroniczna: 31-08-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (58 KB)
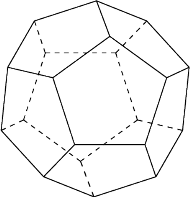
Znajdź na płaszczyźnie skończenie wiele okręgów o rozłącznych wnętrzach i takich, że każdy jest styczny do dokładnie pięciu z pozostałych.

 tej sfery, przeciwległym do punktu
tej sfery, przeciwległym do punktu
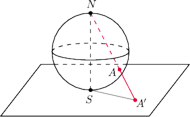
 styczności ze stołem,
zapalamy żarówkę. Zaznaczamy na powierzchni sfery dowolny punkt
styczności ze stołem,
zapalamy żarówkę. Zaznaczamy na powierzchni sfery dowolny punkt
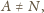 a na stole jego cień
a na stole jego cień
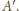 Taki
Taki
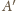 nazywamy
rzutem stereograficznym punktu
nazywamy
rzutem stereograficznym punktu
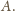 Rzut ten działa na punktach
rozważanej sfery tak, jak inwersja o środku
Rzut ten działa na punktach
rozważanej sfery tak, jak inwersja o środku
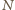 i promieniu
i promieniu
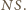
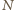 przeprowadza na okręgi oraz zachowuje
styczność.
przeprowadza na okręgi oraz zachowuje
styczność.
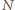 będzie dowolnym z punktów sfery, leżących na zewnątrz
wszystkich okręgów. Rzut stereograficzny z
będzie dowolnym z punktów sfery, leżących na zewnątrz
wszystkich okręgów. Rzut stereograficzny z
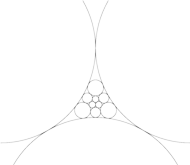
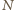 przeprowadza naszą
przestrzenną konfigurację na szukaną płaską konfigurację okręgów (rysunek
obok).
przeprowadza naszą
przestrzenną konfigurację na szukaną płaską konfigurację okręgów (rysunek
obok).