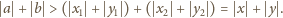Zadanie ZM-1322
o zadaniu...
- Publikacja w Delcie: sierpień 2011
- Publikacja elektroniczna: 31-07-2011
Na płaszczyźnie danych jest
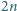różnych punktów:
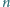białych
oraz
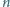czarnych. Żadne trzy nie leżą na jednej prostej. Udowodnić,
że można tak narysować
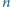odcinków o końcach w danych
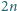punktach, aby końce były różnokolorowe i aby narysowane odcinki
nie przecinały się.
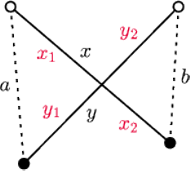
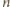odcinków o różnokolorowych końcach możemy
skonstruować na skończenie wiele sposobów (dokładnie
).
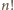Narysujmy go tak, aby suma długości narysowanych odcinków była możliwie
najmniejsza. Wtedy te odcinki są parami rozłączne, bo w przeciwnym przypadku
parę
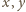przecinających się odcinków (
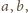zmniejszając jednocześnie
sumę długości wszystkich odcinków. Wynika to łatwo z nierówności
trójkąta:
