LXII Olimpiada Matematyczna»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: LXII OLimpiada Matematyczna.
- Zadanie pochodzi z artykułu LXII Olimpiada Matematyczna
- Publikacja w Delcie: sierpień 2011
- Publikacja elektroniczna: 31-07-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (98 KB)
Okrąg wpisany w trójkąt
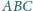jest styczny do boków
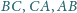odpowiednio w punktach
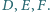Prowadzimy trzy
proste: przez środki odcinków
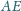i
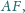przez środki
odcinków
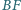i
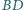oraz przez środki odcinków
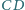i
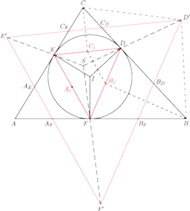
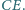Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
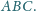
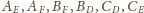będą środkami odcinków
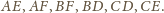Z twierdzenia Talesa wynika, że
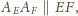
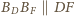i
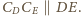Przez
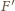oznaczamy punkt wspólny prostych
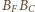i
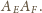Analogicznie definiujemy punkty
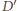i
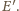Boki
trójkątów
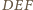i
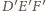są odpowiednio równoległe, więc
punkt
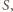w którym przecinają się proste
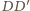i
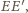jest
środkiem jednokładności w skali
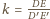przekształcającej trójkąt
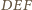na trójkąt
(
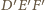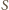leży też na prostej
).
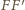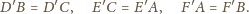
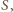w skali
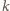przekształca okrąg
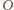opisany na trójkącie
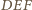na okrąg
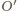opisany na trójkącie
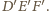Środek okręgu
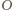leży na prostopadłych do prostych
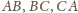przechodzących
przez wierzchołki
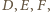więc środek okręgu
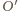leży na
prostopadłych do prostych
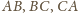przechodzących przez wierzchołki
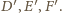Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
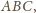więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
