Zadanie ZM-1315
o zadaniu...
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
Dany jest taki pięciokąt wypukły
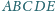 , w którym pola trójkątów
, w którym pola trójkątów
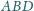 ,
,
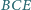 ,
,
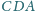 ,
,
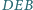 i
i
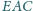 są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.

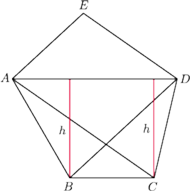
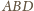 i
i
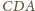 mają równe pola oraz wspólny
bok
mają równe pola oraz wspólny
bok
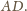 Wobec tego wysokości tych trójkątów poprowadzone do
boku
Wobec tego wysokości tych trójkątów poprowadzone do
boku
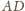 są równe. Ponadto punkty
są równe. Ponadto punkty
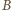 i
i
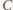 leżą po
tej samej stronie prostej
leżą po
tej samej stronie prostej
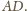 Stąd wniosek, że przekątna
Stąd wniosek, że przekątna
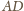 jest
równoległa do boku
jest
równoległa do boku
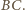 Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
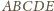 są równoległe do odpowiednich jego
boków
są równoległe do odpowiednich jego
boków