Zadanie ZM-1314
o zadaniu...
- Publikacja w Delcie: maj 2011
- Publikacja elektroniczna: 04-05-2011
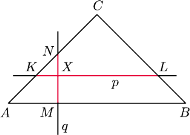
Dany jest prostokątny trójkąt równoramienny
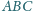 o kącie prostym
przy wierzchołku
o kącie prostym
przy wierzchołku
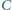 . Znaleźć zbiór takich punktów
. Znaleźć zbiór takich punktów
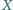 z wnętrza trójkąta
z wnętrza trójkąta
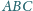 , że jeśli prosta
, że jeśli prosta
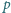 równoległa do
podstawy
równoległa do
podstawy
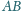 przechodząca przez punkt
przechodząca przez punkt
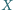 przecina ramiona
przecina ramiona
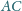 i
i
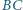 w punktach
w punktach
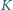 i
i
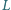 , zaś
, zaś
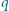 jest prostą
prostopadłą do
jest prostą
prostopadłą do
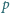 przechodzącą przez
przechodzącą przez
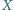 , przecinającą podstawę
, przecinającą podstawę
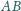 trójkąta w punkcie
trójkąta w punkcie
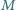 , a ramię w punkcie
, a ramię w punkcie
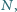 to
to
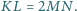

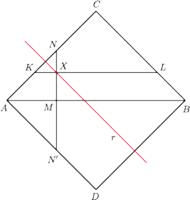
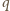 przecina ramię
przecina ramię
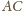 . Rozszerzmy nasz
trójkąt do kwadratu
. Rozszerzmy nasz
trójkąt do kwadratu
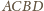 .
.
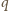 z nowo dorysowanym bokiem kwadratu
oznaczmy przez
z nowo dorysowanym bokiem kwadratu
oznaczmy przez
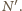 Szukamy takich punktów
Szukamy takich punktów
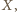 że
że
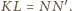 Równoważnie takich, że odcinki
Równoważnie takich, że odcinki
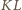 i
i
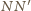 są symetryczne względem prostej
są symetryczne względem prostej
 prostopadłej do
prostopadłej do
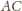 przechodzącej przez
przechodzącej przez
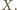 To zachodzi wtedy i tylko wtedy, gdy
trójkąty
To zachodzi wtedy i tylko wtedy, gdy
trójkąty
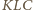 i
i
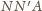 są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
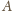 i
i
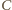 są symetryczne
względem
są symetryczne
względem
 (bo punkty
(bo punkty
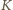 i
i
 zostały skonstruowane tak,
że są symetryczne względem
zostały skonstruowane tak,
że są symetryczne względem
 ).
).