Zadanie ZM-1306
o zadaniu...
- Publikacja w Delcie: marzec 2011
- Publikacja elektroniczna: 02-03-2011
Na boku
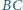 trójkąta
trójkąta
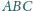 wybrano punkt
wybrano punkt
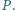 Punkty
Punkty
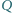 i
i
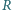 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty
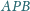 i
i
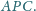 Punkt
Punkt
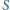 jest punktem styczności okręgu wpisanego w trójkąt
jest punktem styczności okręgu wpisanego w trójkąt
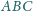 do boku
do boku
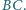 Wykazać, że punkty
Wykazać, że punkty
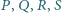 leżą na
jednym okręgu.
leżą na
jednym okręgu.

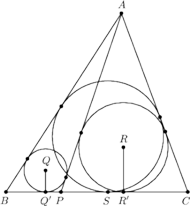
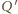 i
i
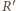 oznaczają rzuty punktów
oznaczają rzuty punktów
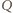 i
i
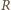 na
prostą
na
prostą
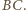 Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
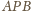 wynika równość
wynika równość
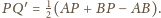 Podobnie mamy
Podobnie mamy
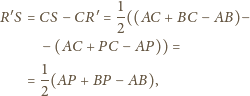
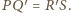 Stąd również
Stąd również
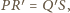 czyli
czyli
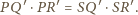
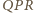 między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
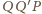 i
i
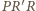 są podobne. W takim
razie
są podobne. W takim
razie
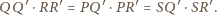
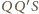 i
i
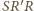 są podobne, więc kąt
są podobne, więc kąt
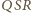 też
jest prosty. To oznacza, że punkty
też
jest prosty. To oznacza, że punkty
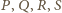 leżą na jednym
okręgu.
leżą na jednym
okręgu.