Zejdźmy na ziemię»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Zejdźmy na ziemię
- Publikacja w Delcie: marzec 2011
- Publikacja elektroniczna: 02-03-2011
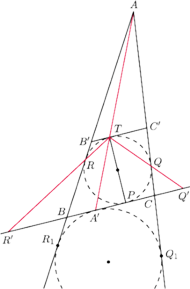
Okrąg wpisany w trójkąt
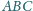 jest styczny do boków
jest styczny do boków
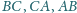 odpowiednio w punktach
odpowiednio w punktach
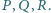 Odcinek
Odcinek
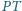 jest średnicą tego
okręgu. Proste
jest średnicą tego
okręgu. Proste
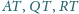 przecinają prostą
przecinają prostą
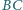 odpowiednio
w punktach
odpowiednio
w punktach
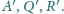 Wykazać, że
Wykazać, że
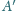 jest środkiem odcinka
jest środkiem odcinka
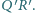

 jest średnicą, to styczna do okręgu wpisanego w punkcie
jest średnicą, to styczna do okręgu wpisanego w punkcie
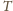 jest równoległa do
jest równoległa do
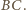 Niech
Niech
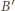 i
i
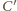 będą punktami
przecięcia tej stycznej z bokami
będą punktami
przecięcia tej stycznej z bokami
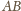 i
i
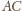 (
(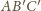 i
i
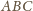 są jednokładne, skąd natychmiast wynika, że
punkt
są jednokładne, skąd natychmiast wynika, że
punkt
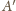 jest punktem styczności okręgu dopisanego z bokiem
jest punktem styczności okręgu dopisanego z bokiem
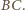 Z równoległości
Z równoległości
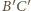 i
i
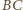 wynika też, że trójkąty
wynika też, że trójkąty
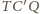 i
i
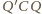 są podobne, a skoro
są podobne, a skoro
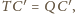 to
to
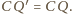 Niech
Niech
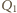 będzie punktem styczności okręgu
dopisanego, stycznego do
będzie punktem styczności okręgu
dopisanego, stycznego do
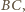 z prostą
z prostą
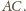 W takim razie
W takim razie
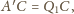 a stąd natychmiast wynika, że
a stąd natychmiast wynika, że
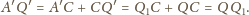
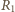 punkt styczności okręgu dopisanego
z bokiem
punkt styczności okręgu dopisanego
z bokiem
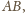 udowodnimy, że
udowodnimy, że
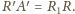 Ale
Ale
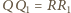 – dowód jest więc zakończony.
– dowód jest więc zakończony.