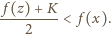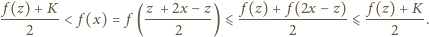Zadanie ZM-1379
o zadaniu...
- Publikacja w Delcie: marzec 2013
- Publikacja elektroniczna: 01-03-2013
Niech funkcja
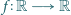 będzie ograniczona z góry, tzn. istnieje taka
liczba
będzie ograniczona z góry, tzn. istnieje taka
liczba
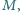 że
że
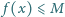 dla każdego
dla każdego
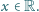 Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
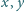 spełniona jest
nierówność
spełniona jest
nierówność
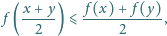
to
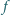 jest funkcją stałą.
jest funkcją stałą.
W szczególności, funkcje wypukłe nie są ograniczone z góry, chyba że są stałe.

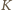 będzie najmniejszą liczbą o tej własności, że
będzie najmniejszą liczbą o tej własności, że
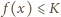 dla
każdej liczby rzeczywistej
dla
każdej liczby rzeczywistej
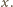 Pokażemy, że wówczas
Pokażemy, że wówczas
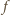 jest
funkcją stałą, równą
jest
funkcją stałą, równą
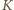 w każdym punkcie. Załóżmy nie wprost, że
dla pewnego
w każdym punkcie. Załóżmy nie wprost, że
dla pewnego
 jest
jest
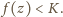 Skoro
Skoro
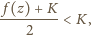
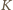 znajdziemy liczbę
znajdziemy liczbę
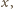 dla której
dla której