VII Olimpiada Matematyczna Gimnazjalistów»Zadanie 1
o zadaniu...
- Zadanie olimpijskie: VII Olimpiada Matematyczna Gimnazjalistów
- Zadanie pochodzi z artykułu VII Olimpiada Matematyczna Gimnazjalistów
- Publikacja w Delcie: czerwiec 2012
- Publikacja elektroniczna: 02-06-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (34 KB)
Wyznacz wszystkie takie liczby rzeczywiste
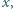 dla których liczby
dla których liczby
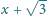 oraz
oraz
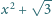 są wymierne.
są wymierne.

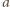 i
i
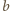 odpowiednio liczby wymierne
odpowiednio liczby wymierne
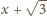 oraz
oraz
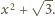 Wówczas
Wówczas
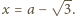 Stąd
otrzymujemy
Stąd
otrzymujemy
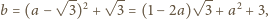
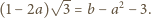
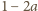 jest różna od zera. Wówczas
jest różna od zera. Wówczas
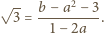
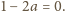 Wobec tego
Wobec tego
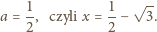
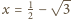 spełnia warunki
zadania. Na mocy powyższego rozumowania jest to jedyna liczba o żądanej
własności.
spełnia warunki
zadania. Na mocy powyższego rozumowania jest to jedyna liczba o żądanej
własności.