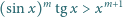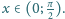Załóżmy, że
 jest taką liczbą, dla której badana nierówność
jest taką liczbą, dla której badana nierówność
 | (1) |
zachodzi dla wszystkich
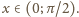 Wiadomo, że
Wiadomo, że
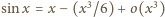 przy
przy
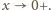 Jeśli więc
Jeśli więc
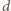 jest
dowolną liczbą większą od 6, to dla
jest
dowolną liczbą większą od 6, to dla
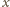 dodatnich, bliskich 0, mamy
dodatnich, bliskich 0, mamy
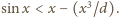 Ponadto,
Ponadto,
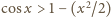 dla
dla
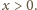 Zatem
Zatem
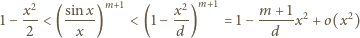
przy
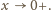 Stąd
Stąd
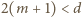 dla każdego
dla każdego
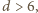 czyli
czyli
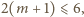 czyli
czyli
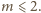
Wykażemy, że i na odwrót, jeśli
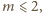 to nierówność (1) zachodzi
dla
to nierówność (1) zachodzi
dla
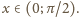 Gdy
Gdy
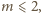 to
to
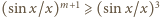 ;
wystarczy więc udowodnić nierówność (1) dla wykładnika
;
wystarczy więc udowodnić nierówność (1) dla wykładnika
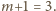 Można ją wówczas przepisać w postaci
Można ją wówczas przepisać w postaci
 | (2) |
– lub równoważnie:
 | (3) |
Funkcja
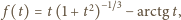 określona dla
określona dla
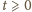 i ciągła
w punkcie 0, ma pochodną
i ciągła
w punkcie 0, ma pochodną
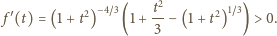
Zatem
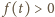 dla
dla
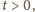 co dowodzi nierówności (3)
i równoważnej jej nierówności (2).
co dowodzi nierówności (3)
i równoważnej jej nierówności (2).
Odpowiedź: Szukane liczby
 to wszystkie liczby
to wszystkie liczby
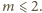
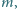 dla których nierówność
dla których nierówność