Rozważmy planszę o wymiarach
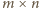 i na każdym polu dokonajmy
losowania: z prawdopodobieństwem
i na każdym polu dokonajmy
losowania: z prawdopodobieństwem
 postawimy tam biały
pionek, a z prawdopodobieństwem
postawimy tam biały
pionek, a z prawdopodobieństwem
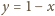 – czarny. Wówczas
prawdopodobieństwo tego, że na każdym z
– czarny. Wówczas
prawdopodobieństwo tego, że na każdym z
 pól wybranej kolumny
stoi biały pionek, jest równe
pól wybranej kolumny
stoi biały pionek, jest równe
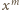 . W takim razie
. W takim razie
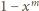 to
prawdopodobieństwo tego, że w tej kolumnie znajdzie się chociaż jeden
pionek czarny, a
to
prawdopodobieństwo tego, że w tej kolumnie znajdzie się chociaż jeden
pionek czarny, a
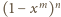 możemy zinterpretować jako szansę na
to, że w każdej kolumnie będzie przynajmniej jeden czarny pionek.
Podobnie
możemy zinterpretować jako szansę na
to, że w każdej kolumnie będzie przynajmniej jeden czarny pionek.
Podobnie
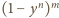 to szansa zdarzenia, że w każdym wierszu jest
co najmniej jeden biały pionek. Zauważmy jednak, że któreś z tych
zdarzeń musi wystąpić, ponieważ jeżeli jakaś kolumna zawiera same
białe pionki, to w każdym wierszu jest już biały pionek. To dowodzi
podanej nierówności.
to szansa zdarzenia, że w każdym wierszu jest
co najmniej jeden biały pionek. Zauważmy jednak, że któreś z tych
zdarzeń musi wystąpić, ponieważ jeżeli jakaś kolumna zawiera same
białe pionki, to w każdym wierszu jest już biały pionek. To dowodzi
podanej nierówności.
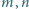 i dla
dowolnych liczb rzeczywistych nieujemnych
i dla
dowolnych liczb rzeczywistych nieujemnych
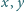 spełniających warunek
spełniających warunek
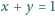 zachodzi nierówność
zachodzi nierówność
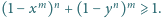

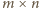 i na każdym polu dokonajmy
losowania: z prawdopodobieństwem
i na każdym polu dokonajmy
losowania: z prawdopodobieństwem
 postawimy tam biały
pionek, a z prawdopodobieństwem
postawimy tam biały
pionek, a z prawdopodobieństwem
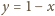 – czarny. Wówczas
prawdopodobieństwo tego, że na każdym z
– czarny. Wówczas
prawdopodobieństwo tego, że na każdym z
 pól wybranej kolumny
stoi biały pionek, jest równe
pól wybranej kolumny
stoi biały pionek, jest równe
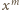 . W takim razie
. W takim razie
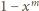 to
prawdopodobieństwo tego, że w tej kolumnie znajdzie się chociaż jeden
pionek czarny, a
to
prawdopodobieństwo tego, że w tej kolumnie znajdzie się chociaż jeden
pionek czarny, a
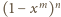 możemy zinterpretować jako szansę na
to, że w każdej kolumnie będzie przynajmniej jeden czarny pionek.
Podobnie
możemy zinterpretować jako szansę na
to, że w każdej kolumnie będzie przynajmniej jeden czarny pionek.
Podobnie
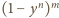 to szansa zdarzenia, że w każdym wierszu jest
co najmniej jeden biały pionek. Zauważmy jednak, że któreś z tych
zdarzeń musi wystąpić, ponieważ jeżeli jakaś kolumna zawiera same
białe pionki, to w każdym wierszu jest już biały pionek. To dowodzi
podanej nierówności.
to szansa zdarzenia, że w każdym wierszu jest
co najmniej jeden biały pionek. Zauważmy jednak, że któreś z tych
zdarzeń musi wystąpić, ponieważ jeżeli jakaś kolumna zawiera same
białe pionki, to w każdym wierszu jest już biały pionek. To dowodzi
podanej nierówności.