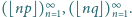Niech
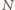 będzie liczbą całkowitą dodatnią. Zastanówmy się, ile jest liczb
mniejszych od
będzie liczbą całkowitą dodatnią. Zastanówmy się, ile jest liczb
mniejszych od
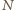 , które występują w obu danych ciągach (każdą liczbę
liczymy tyle razy, ile razy wystąpiła). Otóż nierówność
, które występują w obu danych ciągach (każdą liczbę
liczymy tyle razy, ile razy wystąpiła). Otóż nierówność
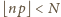 jest
równoważna
jest
równoważna
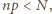 innymi słowy
innymi słowy
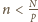 . To oznacza, że
w pierwszym ciągu takich liczb mamy dokładnie
. To oznacza, że
w pierwszym ciągu takich liczb mamy dokładnie
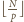 . Analogicznie
w drugim ciągu jest ich
. Analogicznie
w drugim ciągu jest ich
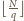 , co łącznie daje
, co łącznie daje
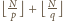 . Dla liczby
niewymiernej
. Dla liczby
niewymiernej
 mamy
mamy
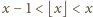 , stąd:
, stąd:
To oznacza, że
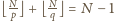 , bo jest to liczba całkowita. Wiemy
w takim razie, że liczb mniejszych od
, bo jest to liczba całkowita. Wiemy
w takim razie, że liczb mniejszych od
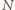 jest w obu tych ciągach
dokładnie
jest w obu tych ciągach
dokładnie
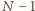 . Podobnie dowodzimy, że liczb mniejszych od
. Podobnie dowodzimy, że liczb mniejszych od
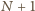 jest dokładnie
jest dokładnie
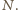 Odejmując te wyniki, wnioskujemy, że
liczba
Odejmując te wyniki, wnioskujemy, że
liczba
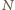 pojawia się w tych ciągach dokładnie raz.
pojawia się w tych ciągach dokładnie raz.
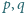 , że
, że
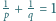 .
Udowodnić, że każda liczba całkowita dodatnia występuje dokładnie raz
w dokładnie jednym z ciągów
.
Udowodnić, że każda liczba całkowita dodatnia występuje dokładnie raz
w dokładnie jednym z ciągów