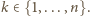Oznaczmy przez
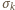 operację polegającą na zmianie znaku na
operację polegającą na zmianie znaku na
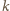 -tej
współrzędnej
-tej
współrzędnej
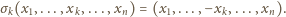
Zauważmy, że dla dowolnego punktu
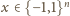 zachodzi równość
zachodzi równość
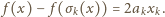
Z drugiej strony, skoro
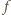 przyjmuje tylko wartości 1 i
przyjmuje tylko wartości 1 i
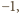 to ta
różnica może przyjmować tylko trzy wartości:
to ta
różnica może przyjmować tylko trzy wartości:
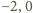 i
i
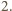 Zatem dla tych
Zatem dla tych
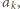 które są niezerowe, musi być
które są niezerowe, musi być
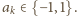
Wykażemy teraz, że funkcja
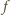 ma dokładnie jeden niezerowy
współczynnik. Załóżmy przeciwnie, że ma przynajmniej dwa, np.
ma dokładnie jeden niezerowy
współczynnik. Załóżmy przeciwnie, że ma przynajmniej dwa, np.
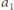 i
i
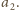 Bez utraty ogólności możemy przyjąć, że
Bez utraty ogólności możemy przyjąć, że
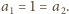 Wówczas, oznaczając przez
Wówczas, oznaczając przez
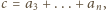 mamy
mamy
Innymi słowy,
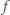 przyjmuje w tych trzech punktach trzy różne
wartości, co przeczy temu, że wartości
przyjmuje w tych trzech punktach trzy różne
wartości, co przeczy temu, że wartości
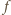 należą do zbioru
dwuelementowego. Zatem
należą do zbioru
dwuelementowego. Zatem
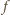 jest postaci
jest postaci
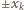 dla pewnego
dla pewnego
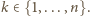
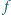 postaci
postaci
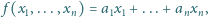
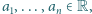 które na zbiorze
które na zbiorze
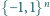 przyjmują
tylko dwie wartości:
przyjmują
tylko dwie wartości:
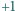 lub
lub
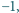 tzn. takie, że jeśli
tzn. takie, że jeśli
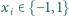 dla
dla
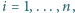 to
to
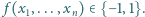

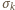 operację polegającą na zmianie znaku na
operację polegającą na zmianie znaku na
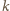 -tej
współrzędnej
-tej
współrzędnej
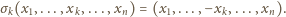
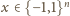 zachodzi równość
zachodzi równość
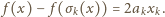
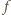 przyjmuje tylko wartości 1 i
przyjmuje tylko wartości 1 i
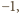 to ta
różnica może przyjmować tylko trzy wartości:
to ta
różnica może przyjmować tylko trzy wartości:
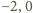 i
i
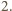 Zatem dla tych
Zatem dla tych
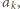 które są niezerowe, musi być
które są niezerowe, musi być
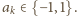
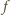 ma dokładnie jeden niezerowy
współczynnik. Załóżmy przeciwnie, że ma przynajmniej dwa, np.
ma dokładnie jeden niezerowy
współczynnik. Załóżmy przeciwnie, że ma przynajmniej dwa, np.
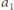 i
i
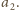 Bez utraty ogólności możemy przyjąć, że
Bez utraty ogólności możemy przyjąć, że
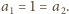 Wówczas, oznaczając przez
Wówczas, oznaczając przez
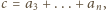 mamy
mamy
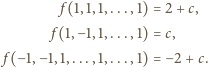
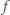 przyjmuje w tych trzech punktach trzy różne
wartości, co przeczy temu, że wartości
przyjmuje w tych trzech punktach trzy różne
wartości, co przeczy temu, że wartości
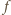 należą do zbioru
dwuelementowego. Zatem
należą do zbioru
dwuelementowego. Zatem
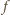 jest postaci
jest postaci
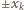 dla pewnego
dla pewnego