Zadanie ZM-1342
o zadaniu...
- Publikacja w Delcie: marzec 2012
- Publikacja elektroniczna: 02-03-2012
Mówimy, że funkcja
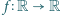 ma cykl długości
ma cykl długości
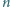 o początku
o początku
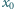 , gdy istnieje takie
, gdy istnieje takie
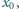 że liczby
że liczby
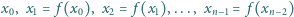 są parami różne, zaś
są parami różne, zaś
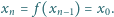
Udowodnić, że jeśli wielomian o współczynnikach całkowitych ma
cykl o początku będącym liczbą całkowitą, to jest on długości
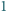 lub
lub
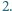

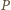 o współczynnikach
całkowitych ma cykl
o współczynnikach
całkowitych ma cykl
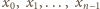 długości
długości
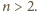 Mamy
Mamy
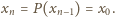 Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
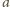 i
i
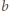 zachodzi
zachodzi
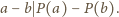
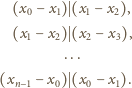
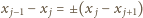
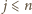 (przyjmujemy, że
(przyjmujemy, że
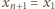 ). Znak „–” jest
wykluczony, gdyż liczby
). Znak „–” jest
wykluczony, gdyż liczby
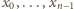 są parami różne. Mamy więc
są parami różne. Mamy więc
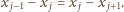 Oznacza to, że ciąg
Oznacza to, że ciąg
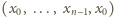 jest
arytmetyczny. Musi on być stały, co daje sprzeczność.
jest
arytmetyczny. Musi on być stały, co daje sprzeczność.