Neon»Zadanie
o zadaniu...
- Zadanie pochodzi z artykułu Neon
- Publikacja w Delcie: sierpień 2011
- Publikacja elektroniczna: 31-07-2011
Neon składa się z dwóch słów. Na ile sposobów można zgasić niektóre litery w neonie, tak by litery, które pozostaną zapalone, w obu słowach układały się w ten sam niepusty podciąg? Ile różnych podciągów da się w ten sposób uzyskać?
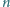 -kąt. Na początku żadna przekątna nie jest
narysowana. Zadaniem jest opracowanie struktury danych, która umożliwi
optymalne obsłużenie zapytań:
-kąt. Na początku żadna przekątna nie jest
narysowana. Zadaniem jest opracowanie struktury danych, która umożliwi
optymalne obsłużenie zapytań:
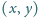 — sprawdza, czy między punktami
— sprawdza, czy między punktami
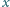 i
i
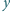 jest narysowana przekątna,
jest narysowana przekątna,
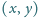 — rysuje przekątną pomiędzy punktami
— rysuje przekątną pomiędzy punktami
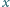 i
i
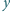 — o ile nie przecina ona żadnej innej narysowanej przekątnej,
— o ile nie przecina ona żadnej innej narysowanej przekątnej,
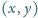 — usuwa przekątną między punktami
— usuwa przekątną między punktami
 i
i
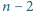 trójek
trójek
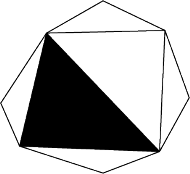
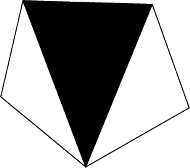
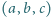 definiujących kolejne trójkąty (wierzchołki wielokąta są
ponumerowane kolejno od 1 do n). Czarny trójkąt jest wymieniony jako
pierwszy. Musimy odpowiedzieć na pytanie: który gracz ma strategię
wygrywającą?
definiujących kolejne trójkąty (wierzchołki wielokąta są
ponumerowane kolejno od 1 do n). Czarny trójkąt jest wymieniony jako
pierwszy. Musimy odpowiedzieć na pytanie: który gracz ma strategię
wygrywającą?
 (jeśli
(jeśli
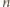 jest parzyste wygrywa gracz, który rozpoczyna grę), a i sama
strategia jest prosta i brzmi: odcinaj cokolwiek, byle nie odsłonić czarnego
trójkąta z dwóch stron. Całe zadanie można więc rozwiązać w czasie stałym,
sprawdzając jedynie czy czarny trójkąt leży na brzegu (jego współrzędne
to wówczas trzy kolejne liczby modulo
jest parzyste wygrywa gracz, który rozpoczyna grę), a i sama
strategia jest prosta i brzmi: odcinaj cokolwiek, byle nie odsłonić czarnego
trójkąta z dwóch stron. Całe zadanie można więc rozwiązać w czasie stałym,
sprawdzając jedynie czy czarny trójkąt leży na brzegu (jego współrzędne
to wówczas trzy kolejne liczby modulo
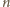 ), a jeśli nie, to czy
), a jeśli nie, to czy
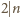 . Nie trzeba, a wręcz nie warto, wczytywać nadmiarowego opisu
triangulacji!
. Nie trzeba, a wręcz nie warto, wczytywać nadmiarowego opisu
triangulacji!
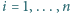 ) umowę, w której określona jest
pewna liczba
) umowę, w której określona jest
pewna liczba
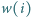 : mianowicie, jeśli listonosz odwiedzi wieś
numer
: mianowicie, jeśli listonosz odwiedzi wieś
numer
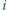 jako
jako
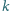 -tą w kolejności (tzn. odwiedził wcześniej
dokładnie
-tą w kolejności (tzn. odwiedził wcześniej
dokładnie
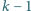 różnych innych wsi) oraz
różnych innych wsi) oraz
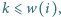 to wieś
dopłaca poczcie
to wieś
dopłaca poczcie
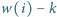 EUR, a jeśli
EUR, a jeśli
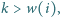 to poczta
karnie płaci wsi
to poczta
karnie płaci wsi
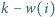 EUR. Jak wyznaczyć trasę listonosza, aby
zmaksymalizować zysk (ew. zminimalizować stratę) poczty? Na wejściu
mamy daną liczbę wsi
EUR. Jak wyznaczyć trasę listonosza, aby
zmaksymalizować zysk (ew. zminimalizować stratę) poczty? Na wejściu
mamy daną liczbę wsi
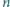 , opis grafu dróg i umówione wartości
, opis grafu dróg i umówione wartości
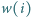 ,
,
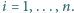
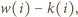
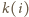 jest pozycją tej wioski na liście kolejno odwiedzonych wsi przy
danej trasie listonosza. Ciąg
jest pozycją tej wioski na liście kolejno odwiedzonych wsi przy
danej trasie listonosza. Ciąg
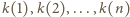 jest permutacją liczb
jest permutacją liczb
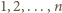 – każda wioska została odwiedzona jako któraś z kolei.
Zatem suma wszystkich wpłat wynosi:
– każda wioska została odwiedzona jako któraś z kolei.
Zatem suma wszystkich wpłat wynosi:
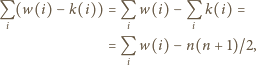
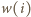 i cała otoczka związana z optymalizacją służyły tylko mydleniu oczu
rozwiązującego!
i cała otoczka związana z optymalizacją służyły tylko mydleniu oczu
rozwiązującego!
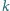 województw
i zawierające
województw
i zawierające
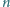 miast. W tym państwie jest
miast. W tym państwie jest
 dróg,
z których każda łączy jakąś parę miast. Naszym zadaniem jest tak wybrać
stolice województw, aby każde województwo miało dokładnie jedną
stolicę (będącą jednym z miast tegoż województwa), a każda z dróg
miała jakąś stolicę na co najmniej jednym swym końcu. Wiadomo, że
każda droga łączy dwa różne miasta, każde województwo zawiera
co najmniej jedno miasto, a każde miasto należy do dokładnie jednego
województwa.
dróg,
z których każda łączy jakąś parę miast. Naszym zadaniem jest tak wybrać
stolice województw, aby każde województwo miało dokładnie jedną
stolicę (będącą jednym z miast tegoż województwa), a każda z dróg
miała jakąś stolicę na co najmniej jednym swym końcu. Wiadomo, że
każda droga łączy dwa różne miasta, każde województwo zawiera
co najmniej jedno miasto, a każde miasto należy do dokładnie jednego
województwa.
 kamiennych bloków różnych rozmiarów.
Mamy obliczyć, na ile sposobów można zbudować z tych bloków wieżę,
jeżeli należy użyć ich wszystkich, a jeden blok można położyć na drugim
tylko wtedy, gdy rozmiar górnego jest nie większy niż rozmiar dolnego
powiększony o ustaloną liczbę dodatnią
kamiennych bloków różnych rozmiarów.
Mamy obliczyć, na ile sposobów można zbudować z tych bloków wieżę,
jeżeli należy użyć ich wszystkich, a jeden blok można położyć na drugim
tylko wtedy, gdy rozmiar górnego jest nie większy niż rozmiar dolnego
powiększony o ustaloną liczbę dodatnią
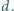 Wynik należy zwrócić
modulo jakaś nieduża liczba całkowita.
Wynik należy zwrócić
modulo jakaś nieduża liczba całkowita.
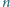 nauczycieli i ogłoszono nabór do
nauczycieli i ogłoszono nabór do
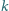 klas. W szkole będzie nauczanych
klas. W szkole będzie nauczanych
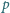 przedmiotów. Każdy przedmiot ma przypisanego nauczyciela, który
będzie go wykładał, oraz klasę, która będzie na te wykłady uczęszczała.
Każdego dnia na dany przedmiot ma być przeznaczona jedna godzina lekcyjna.
Należy wyznaczyć plan zajęć w szkole, tak by zminimalizować czas,
w którym w szkole przebywają uczniowie.
przedmiotów. Każdy przedmiot ma przypisanego nauczyciela, który
będzie go wykładał, oraz klasę, która będzie na te wykłady uczęszczała.
Każdego dnia na dany przedmiot ma być przeznaczona jedna godzina lekcyjna.
Należy wyznaczyć plan zajęć w szkole, tak by zminimalizować czas,
w którym w szkole przebywają uczniowie.