Nie takie sztuczne neurony
Niemal każdy wykład wprowadzający w zagadnienie sztucznych sieci neuronowych zaczyna się anegdotą o zaczerpnięciu tego pojęcia z anatomii mózgu...

Najprostszy model matematycznej jednostki zwanej "sztucznym neuronem" opisuje równanie:
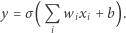 |
W analogii do biologicznych komórek neuronowych mamy do czynienia z sumą informacji 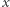 (przesyłanej z komórek presynaptycznych do postsynaptycznych) z odpowiednimi wagami
(przesyłanej z komórek presynaptycznych do postsynaptycznych) z odpowiednimi wagami 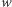 (siła połączeń synaptycznych), na którą działa funkcja nieliniowa
(siła połączeń synaptycznych), na którą działa funkcja nieliniowa 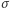 (uwolnienie potencjału czynnościowego po osiągnięciu wartości progowej).
(uwolnienie potencjału czynnościowego po osiągnięciu wartości progowej).
Historia wzajemnych wpływów uczenia maszynowego i neuronauki jest jednak znacznie dłuższa i o wiele bardziej skomplikowana. Szczególnie wyraźnie zaznacza się to w ostatnich latach, gdy niezwykłą popularność zdobywają tzw. głębokie sieci neuronowe (deep neural networks). Swoją strukturą coraz bardziej przypominają one skomplikowane układy przetwarzające informacje w mózgu. W niedawnym wydaniu periodyku naukowego Neuron rolę współpracy naukowców z tych dwóch obszarów wiedzy podkreślał sam Demmis Hassabis, współzałożyciel DeepMind. Dla przypomnienia, ta należąca do Google firma zasłynęła opracowaniem programu AlphaGo, który jako pierwszy automat wygrał (w 2016 roku) z arcymistrzem gry w Go, Lee Sedolem. Ciekawostką jest fakt, że AlphaGo został uhonorowany za to przez południowokoreańską federację dziewiątym danem. Gra planszowa Go uznawana jest przez ekspertów za najtrudniejszą na świecie!

Jednym z najprostszych modeli matematycznych znajdującym zastosowanie w obu wspomnianych dziedzinach jest tzw. sieć Hopfielda. W oryginalnym sformułowaniu dyskretna sieć Hopfielda składa się z 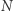 neuronów, z których każdy łączy się z każdym i może przybrać jeden z dwóch stanów:
neuronów, z których każdy łączy się z każdym i może przybrać jeden z dwóch stanów: 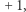 lub
lub 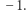 Przez
Przez ![vi[t]](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/4x-719109b6b9f0bb4074a12de286db9742e9d5f6a5-im-33,33,33-FF,FF,FF.gif) oznaczać będziemy stan
oznaczać będziemy stan 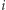 -tego neuronu w chwili
-tego neuronu w chwili 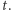 Wagę połączenia między
Wagę połączenia między 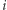 -tym i
-tym i 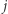 -tym neuronem oznaczamy przez
-tym neuronem oznaczamy przez 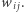 Zakładamy, że wagi są symetryczne
Zakładamy, że wagi są symetryczne 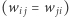 oraz że neuron nie wpływa sam na siebie
oraz że neuron nie wpływa sam na siebie 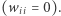 Stan jednostki
Stan jednostki 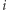 w chwili
w chwili 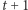 w zależności od stanu układu w chwili
w zależności od stanu układu w chwili 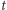 opisuje się równaniem:
opisuje się równaniem:
![N vi[t+ 1] = sgn( Q wijvj[t]) j 1](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/15x-719109b6b9f0bb4074a12de286db9742e9d5f6a5-dm-33,33,33-FF,FF,FF.gif) |
gdzie funkcja 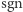 przyjmuje wartość
przyjmuje wartość 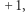 gdy jej argument jest większy od zera, bądź
gdy jej argument jest większy od zera, bądź 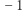 w przeciwnym przypadku. Wyrażenie
w przeciwnym przypadku. Wyrażenie 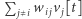 można interpretować jako ekscytację jednostki
można interpretować jako ekscytację jednostki 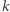 - to znaczy, że w zależności od znaku ekscytacji nastąpi aktywacja
- to znaczy, że w zależności od znaku ekscytacji nastąpi aktywacja 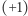 bądź deaktywacja
bądź deaktywacja 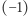 jednostki. Wyrażenie to będziemy oznaczać przez
jednostki. Wyrażenie to będziemy oznaczać przez ![|εi[t].](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/23x-719109b6b9f0bb4074a12de286db9742e9d5f6a5-im-33,33,33-FF,FF,FF.gif)
Dla tak zdefiniowanej sieci określamy energię układu jako:
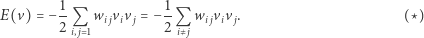 |
Zakładamy, że aktualizacja stanu następuje w sposób asynchroniczny, to znaczy żadne dwa neurony nie są włączane bądź wyłączane w tym samym momencie. Wówczas zmiana energii przy aktualizacji jednostki 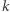 wynosi:
wynosi:
![∆Ek = Ek(v[t+ 1])− Ek(v[t]) = − Q wkjvk[t jxk = (vk[t] −vk[t +1])Q wkjvj[t] jxk](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/3x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-dm-33,33,33-FF,FF,FF.gif) |
Teraz rozpatrzmy dwa przypadki. Kiedy uczenie nie następuje, nie zmienia się stan układu, czyli ![vk[t] = vk[t+ 1].](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/4x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) Mamy zatem
Mamy zatem 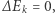 czyli
czyli ![|E (v [t+ 1]) = E (v [t]). k k k k](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/6x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) W przeciwnym przypadku musimy rozważyć kolejne dwie możliwości. Ponieważ nastąpiła zmiana układu:
W przeciwnym przypadku musimy rozważyć kolejne dwie możliwości. Ponieważ nastąpiła zmiana układu:
- dla
![|εk[t] < 0](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/8x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) mamy
mamy ![vk[t] = +1,](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/9x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) a
a ![vk[t +1] =− 1](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/10x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) ;
; - dla
![|εk[t] > 0](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/12x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) mamy
mamy ![vk[t] = − 1,](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/13x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) a
a ![vk[t +1] = +1.](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/14x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif)
Za każdym razem wyrażenie ![(vk[t]− vk[t+ 1])](/math/temat/informatyka/sztuczna_inteligencja/2018/10/22/Nie_takie_sztuczne_neurony/15x-4c955293b1c2f9be960db55e76b64d6e1ee7a85b-im-33,33,33-FF,FF,FF.gif) ma przeciwny znak do wartości ekscytacji. Pokazaliśmy zatem, że
ma przeciwny znak do wartości ekscytacji. Pokazaliśmy zatem, że 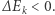 W każdym przypadku energia będzie maleć, a że liczba stanów sieci jest skończona, w skończonym czasie zbiegnie do stanu minimum lokalnego (tzn. niemożliwego do "poprawienia" poprzez opisaną aktywność neuronów). Będzie to tzw. stan stabilny.
W każdym przypadku energia będzie maleć, a że liczba stanów sieci jest skończona, w skończonym czasie zbiegnie do stanu minimum lokalnego (tzn. niemożliwego do "poprawienia" poprzez opisaną aktywność neuronów). Będzie to tzw. stan stabilny.
Jak w takim razie sieć Hopfielda może się czegokolwiek "nauczyć"? W najprostszym wydaniu rzecz opiera się na regule uczenia Hebba, opracowanej już w latach 50. XX wieku przez kanadyjskiego psychologa Donalda Hebba. Mówi ona o tym, że jeśli neuron 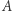 systematycznie pobudza neuron
systematycznie pobudza neuron 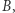 to połączenie synaptyczne między nimi staje się silniejsze (po angielsku często jest to podawane w zgrabnej formie: fire together, wire together). Ta prosta hipoteza została potwierdzona kilkanaście lat po jej sformułowaniu, poprzez odkrycie paradygmatu długotrwałych wzmocnień synaptycznych. Niewątpliwą zaletą reguły Hebba jest fakt, iż w prosty sposób łączy idee z neurobiologii i psychologii, a także stanowi dobry model pamięci asocjacyjnej. Szczególnym przykładem takiej pamięci może być warunkowanie zastosowane w słynnym eksperymencie Pawłowa. Powtarzana ekspozycja psa na miskę z jedzeniem wraz z dźwiękiem dzwonka skutkuje wzmożonym wydzielaniem śliny w reakcji wyłącznie na dźwięk dzwonka.
to połączenie synaptyczne między nimi staje się silniejsze (po angielsku często jest to podawane w zgrabnej formie: fire together, wire together). Ta prosta hipoteza została potwierdzona kilkanaście lat po jej sformułowaniu, poprzez odkrycie paradygmatu długotrwałych wzmocnień synaptycznych. Niewątpliwą zaletą reguły Hebba jest fakt, iż w prosty sposób łączy idee z neurobiologii i psychologii, a także stanowi dobry model pamięci asocjacyjnej. Szczególnym przykładem takiej pamięci może być warunkowanie zastosowane w słynnym eksperymencie Pawłowa. Powtarzana ekspozycja psa na miskę z jedzeniem wraz z dźwiękiem dzwonka skutkuje wzmożonym wydzielaniem śliny w reakcji wyłącznie na dźwięk dzwonka.
Regułę Hebba do zapamiętania wzorca opisanego binarnym wektorem  można zapisać jako:
można zapisać jako:
 |
Zwróćmy uwagę, że przy tak dobranych wagach najmniejsza wartość energii określonej wzorem 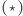 przyjmowana jest dla
przyjmowana jest dla 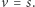 Ponieważ opisany wcześniej proces uczenia stabilizuje się w minimach lokalnych, możemy mieć nadzieję, że będzie on "zbliżać" wektor
Ponieważ opisany wcześniej proces uczenia stabilizuje się w minimach lokalnych, możemy mieć nadzieję, że będzie on "zbliżać" wektor  do
do 

Rys. 1 Zapamiętane wzorce

Rys. 2 Rekonstrukcja litery "C" w trzech krokach
W ogólności, możemy zapamiętać więcej niż jeden wzór. Na przykład, dla 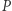 wzorców
wzorców 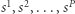 reguła Hebba przyjmuje postać:
reguła Hebba przyjmuje postać:
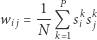 |
co jest odpowiednikiem pamięci skojarzeniowej. Można udowodnić, że pojemność takiej sieci to 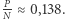 Oznacza to, że sieć złożona z 1000 węzłów jest w stanie zapamiętać maksymalnie około 138 wzorców. Grafika na marginesie pokazuje przykład rekonstrukcji litery "C" dla sieci pamiętającej trzy wzorce. Osiągnięcie lokalnego minimum w sieci Hopfielda jest gwarantowane. Często zdarza się jednak utknięcie w minimum fałszywym, a zatem rozpoznanie wzorca, którego de facto sieć nie była nauczona. Nie zmienia to jednak faktu, iż z powodzeniem sieci te stosuje się do odszumiania obrazów, dekonwolucji danych, rozpoznawania wzorców, a także w problemach optymalizacyjnych.
Oznacza to, że sieć złożona z 1000 węzłów jest w stanie zapamiętać maksymalnie około 138 wzorców. Grafika na marginesie pokazuje przykład rekonstrukcji litery "C" dla sieci pamiętającej trzy wzorce. Osiągnięcie lokalnego minimum w sieci Hopfielda jest gwarantowane. Często zdarza się jednak utknięcie w minimum fałszywym, a zatem rozpoznanie wzorca, którego de facto sieć nie była nauczona. Nie zmienia to jednak faktu, iż z powodzeniem sieci te stosuje się do odszumiania obrazów, dekonwolucji danych, rozpoznawania wzorców, a także w problemach optymalizacyjnych.
Co najważniejsze jednak, idee Donalda Hebba przyczyniły się do powstania modelu równoległego rozproszonego przetwarzania informacji, czyli tzw. koneksjonimzu, spopularyzowanego w latach 80. przez naukowców Uniwersytetu Stanforda: Jamesa McClellanda i Davida Rumelharta. Sieć Hopfielda jest najlepszym przykładem takiego modelu. Istnieje przekonanie, że właśnie z koneksjonizmu wyewoluowała dziedzina głębokich sieci neuronowych. Nic dziwnego, skoro do zwolenników tej idei należy sam Geoffrey Hinton, absolwent psychologii kognitywnej, uważany za ojca chrzestnego deep learning'u. Przykłady interakcji neuronauki i uczenia maszynowego można mnożyć bez końca. Nie wspomniałem tu, na przykład, o klasyfikatorach, wykorzystywanych do dekodowania sygnałów pochodzących z mózgu. Na uwagę zasługują również próby interpretacji działania sztucznych sieci neuronowych, gdzie wykorzystywane są modele kognitywne. Cieszy więc zacieśnianie się współpracy między badaczami obu dziedzin, co pomaga w wypracowaniu wspólnego języka. Cel przecież jest zbieżny: zrozumieć, jak uczy się człowiek, by sprawniej mogła uczyć się maszyna.