Zachęcamy bardzo wszystkich Czytelników do próby rozwiązania zagadki przed przeczytaniem dalszej części tekstu!

Zanim dojdziemy do rozwiązania, spróbujmy zastosować typową taktykę: rozważmy małe przypadki. Co się więc stanie, gdy dokładnie jedno dziecko - Adaś - będzie umazane błotem? Adaś zorientuje się natychmiast, że to o niego chodzi, bo wszyscy inni mają czyste twarze. Natomiast jego rodzeństwo, widząc umazanego Adasia, nie będzie wiedziało, czy oni są czyści, czy brudni. A więc na pierwsze pytanie taty rękę podniesie tylko Adaś. Po tym, gdy pozostałe dzieci zobaczą, że Adaś podniósł rękę, zorientują się, że tylko on jest umazany. W przeciwnym bowiem przypadku nie mógłby się zorientować, że tak jest. Zatem na drugie pytanie taty już wszyscy podniosą ręce.

No dobrze, a co będzie, gdy brudni będą zarówno Adaś, jak i Basia, a pozostali będą czyści? Przy pierwszym pytaniu taty nikt nie podniesie ręki, bo każde z dzieci będzie widziało kogoś umazanego: Adaś i Basia siebie nawzajem, a pozostałe dzieci ich oboje. Potem zdarzy się jednak coś ciekawego. Basia pomyśli w następujący sposób: "Gdybym ja była czysta, to Adaś widziałby same czyste twarze i zorientował się, że w związku z tym musi być brudny. I wtedy podniósłby rękę przy pierwszym pytaniu. Nie zrobił tego jednak, więc moja twarz musi być umazana". Basia w związku z tym podniesie rękę przy drugim pytaniu taty, oczywiście analogicznie pomyśli i zrobi Adaś. Pozostałe dzieci będą widziały dwójkę brudnego rodzeństwa, więc nie będą miały powodu, żeby po pierwszym głosowaniu pomyśleć tak jak Adaś i Basia. Nie będą też miały żadnych przesłanek (do chwili drugiego pytania), że one są czyste, więc przy drugim pytaniu nie podniosą rąk. Po nim jednak natychmiast zorientują się, że Adaś i Basia mogli przeprowadzić swoje rozumowanie i zrozumieć, że mają umazane twarze, tylko o ile jedynie oni byli brudni - czyli wszyscy pozostali są czyści. A więc przy trzecim pytaniu taty podniosą ręce wszystkie dzieci.

Być może Domyślni Czytelnicy zaczynają już powoli podejrzewać, jak będzie w przypadku ogólnym. Przyjrzyjmy się jednak sytuacji, gdy brudnych jest trójka dzieci: Adaś, Basia i Czarek. Czarek widzi, że (oprócz, być może, niego) brudni są tylko Adaś i Basia. Po drugim pytaniu taty widzi jednak, że nie podnieśli oni rąk, czyli nie są jedynymi z umazaną twarzą. Nie można już mieć dłużej wątpliwości: on też należy do tych ubrudzonych. A zatem Czarek, a także Adaś i Basia, podniosą ręce przy trzecim pytaniu taty. Pozostałe dzieci zorientują się dopiero potem, że ich twarze są czyste i zgłoszą to przy czwartym pytaniu.

Nietrudno zauważyć, że powyższe rozumowanie można prowadzić dalej. Przy dokładnie 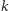brudnych dzieciach podniosą one ręce przy 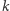-tym pytaniu, a te czyste przy pytaniu 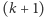-szym. Ale czy to rozwiązuje sprawę? Wielu Czytelników zapewne zgodzi się, że tak konkretnie to ciężko się przyczepić do jakiegoś argumentu, ale nadal problem wydaje się skrywać jakieś tajemnice.

Można przykładowo mieć następującą wątpliwość. Przypuśćmy, że liczba ubrudzonych dzieci jest większa niż jeden, wtedy każdy wie, że ktoś jest umazany błotem, bo po prostu go widzi. Wydaje się więc, że tata - przychodząc i informując o tym - nie odkrywa Ameryki, mówi coś, o czym wie każdy, więc nie wnosi żadnej nowej informacji. Czy mógłby zatem ominąć początkowe stwierdzenie i zacząć od zadawania pytań, kto wie, czy jest brudny? Chwila zastanowienia prowadzi do konkluzji, że nie, samo zadawanie pytań o stan czystości do niczego nie doprowadzi. Dzieci, razem zresztą ze zbyt optymalizującym tatą, spędziłyby całe popołudnie na monotonnej grze w niepodnoszenie rąk. Cóż więc wniosło powiedzenie faktu, który znał każdy?

Okazuje się, że jednak coś istotnego wniosło. Wyjaśnijmy to najpierw dla dwójki brudnych dzieci. Owszem, każdy wiedział, że ktoś jest brudny. Nie każdy jednak wiedział, czy każdy wie, że ktoś jest brudny. Przykładowo Adaś nie wiedział, czy Basia wie, że ktoś jest brudny. No bo gdyby Adaś nie był brudny, to Basia nie widziałaby nikogo brudnego. A co dla trójki brudnych dzieci: Adasia, Basi i Czarka? Wówczas każdy wie, że każdy wie, że ktoś jest brudny. Ale nie każdy wie, czy każdy wie, czy każdy wie, że ktoś jest brudny! Przykładowo Adaś nie wie, czy Basia wie, czy Czarek wie, że jest ktoś brudny. Bo gdyby Adaś był czysty, to jedynie Basia i Czarek byliby brudni i wtedy Basia nie wiedziałaby, czy Czarek widzi kogokolwiek brudnego. Uogólniając te spostrzeżenia, widzimy więc, że to, co tata wniósł do sprawy to fakt, że każdy wie, że każdy wie, że każdy wie... i tak powtórzone dowolnie wiele razy, że ktoś jest brudny!

Nasze rozważania przydają się nie tylko do tego, żeby na imprezie u znajomych zabłysnąć nieoczywistą zagadką. W roku 1997 Joseph Halpern i Yoram Moses otrzymali prestiżową Nagrodę Gödla za pracę nad wiedzą, a w szczególności wiedzą powszechną (ang. common knowledge) i zastosowaniem swojej teorii do dziedziny systemów rozproszonych. Możemy zamienić dzieci z zagadki na komputery, które razem wykonują pewne obliczenia i komunikują się przez sieć. Nie zawsze "wiedzą" one, co "wiedzą" inne komputery, mogą się dowiedzieć jedynie, jeśli dostaną jakiś komunikat. W analizie programów, które są wykonywane przez sieć komputerową (tzn. przeznaczonych do obliczeń rozproszonych), zasadniczą rolę odgrywa właśnie pojęcie wiedzy. Kluczowym spostrzeżeniem autorów artykułu była obserwacja, że nieformalne pojęcie wiedzy da się ująć w precyzyjne matematyczne ramy. W szczególności wiedza powszechna została doprecyzowana właśnie jako sytuacja, gdy dla dowolnego 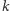zachodzi: "każdy wie" powtórzone 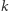razy o pewnym interesującym nas fakcie. Wcześniej, oczywiście, trzeba było zdefiniować formalnie, co to znaczy, że komputer coś wie, ale w to nie będziemy się teraz wgłębiać.

Praca Halperna i Mosesa miała wielki wpływ na dziedzinę obliczeń rozproszonych. Zainspirowała także nowe badania w kryptografii i sztucznej inteligencji. Może czeka nas w przyszłości jeszcze więcej ważnych odkryć, których podstawą są fenomeny możliwe do dostrzeżenia bez żadnego zaawansowanego aparatu matematycznego. A kto wie, może nawet dokonane przez Czytelników Delty.