W pracy [1] autorzy przedstawiają nową strategię kampanii uodporniającej sieć składającą się z bardzo dużej liczby węzłów 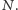Przyjmuje się, że 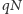węzłów jest zaszczepionych, a pozostałe są podatne na infekcję. Rozprzestrzenianie się zarazy zależy od stopnia jej zaraźliwości, przebiegu infekcji, frakcji 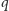zaszczepionych węzłów oraz rodzaju sieci. Rozmiar epidemii (wywołanej jednym ogniskiem) jest jednak zawsze ograniczony z góry przez (względny) rozmiar 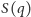największego klastra podatnych węzłów. Dla dużych sieci 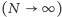celem uodporniania jest ich takie rozdrobnienie, żeby 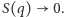Próg immunizacji 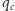jest zdefiniowany jako najmniejsza wartość 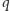pozwalająca ten cel osiągnąć. Im mniejsza wartość 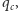tym bardziej efektywna jest rozpatrywana strategia.

Optymalne jest zaszczepienie tylko tych węzłów, które można uważać za tzw. główne węzły blokujące (superblockers), których odblokowanie powoduje istotny wzrost 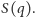Pogląd, że są to jednocześnie główne węzły komunikacyjne (superspreaders) nie jest, w ogólności, poprawny, bo węzeł będący elementem silnie rozgałęzionego fragmentu sieci może być świetnym komunikatorem, ale słabym węzłem blokującym, ze względu na łatwość jego obejścia. Wyszukanie węzłów każdego z tych typów jest przypuszczalnie problemem NP-zupełnym. Z tego względu w przypadku dużych sieci potrzebna jest jakaś heurystyczna metoda ich wyznaczania. Zazwyczaj tworzony jest pewien ranking węzłów w oparciu o charakterystykę tylko jego najbliższego lub o charakterystykę bliższego i dalszego otoczenia.

W pracy [1] punktem wyjścia jest wirtualne zaszczepienie wszystkich węzłów 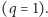Następnie węzły są stopniowo zamieniane z zaszczepionych na podatne, począwszy od uznanych za najmniej niebezpieczne z punktu widzenia rozprzestrzeniania się epidemii. Podejście to jest związane z koncepcją wybuchowego przesiąkania (ang: explosive percolation) [2].

Chodzi o obserwację gwałtownej (nieciągłej) zmiany stopnia skomunikowania sieci po dodaniu niewielkiej liczby połączeń, jeżeli proces ten jest przypadkowy, ale prawdopodobieństwo tworzenia połączeń zależy nie tylko od cech najbliższego otoczenia danego miejsca sieci.

Używane były dwa rankingi wykorzystujące w różnym stopniu lokalną i nielokalną informację do określenia konsekwencji przekształcenia danego węzła z zaszczepionego na podatny. Autorzy twierdzą, że sprawdzili niewielką zależność wyniku od konkretnej realizacji obu używanych schematów. Jeden był używany dla dużych wartości 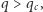a drugi dla małych 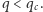Autorzy uważają, że konieczność używania przynajmniej dwóch schematów do uzyskania optymalnej strategii jest pochodną komplikacji obliczeniowej rozpatrywanego problemu. W każdym kroku rozpatrywana była tylko skończona liczba węzłów (rzędu tysiąca), z których był wybierany jeden. Z tego względu algorytm działa szybko (w czasie niemal proporcjonalnym do 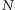), co powoduje, że bez problemu radzi sobie nawet z bardzo dużymi sieciami, osiągając najmniejsze wartości progu immunizacji 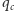spośród opublikowanych algorytmów tego typu.

Jego działanie zostało przetestowane na szeregu sztucznych sieci oraz na kilku rzeczywistych przykładach. Pierwszym z rozpatrywanych był zapis transportów rogacizny w Szkocji w latach 2005-2007, a ostatnim sieć współautorstwa w społeczności fizyków wysokich energii. Ciekawe może być porównanie wyników dla obu tych sieci. Szczególnie dla kogoś, kto jest węzłem jednej z nich. Z tego punktu widzenia pocieszające jest, że badanie dotyczyło sytuacji przed wystąpieniem zarazy, bo mniej więcej wiadomo, jak wygląda "szczepienie" w sieci transportu rogacizny w trakcie rozwoju epidemii. Jeżeli chodzi o zamieszczone w pracy [1] (i jej suplemencie) ilustracje dotyczące obu sieci, to jakościowo niewiele się one różnią. Poza jednym szczegółem. Dla rogacizny mamy zaledwie 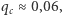natomiast dla fizyków niemal 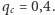W tym drugim przypadku mówienie o braku epidemii nie odpowiada zresztą rzeczywistości. Jest już za późno np. na powstrzymanie wirusa supersymetrii. Żeby tego dokonać, trzeba było odpowiednio wcześnie (prawie pół wieku temu) wyeliminować 40% rozpatrywanej społeczności.