Złoty podział odcinka a ładowanie akumulatora samochodowego
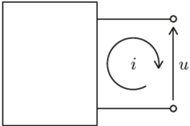
Rys. 1
Akumulator samochodowy jest jednym z wielu źródeł energii używanych w praktyce. Źródłami energii elektrycznej są również ogniwa, prądnice - maszyny prądu stałego, alternatory, turbogeneratory itd. Każde źródło energii elektrycznej możemy sobie wyobrazić jako "skrzynkę" dostępną z zewnątrz poprzez parę końcówek, tworzących tzw. "port energetyczny" (Rys. 1), na którym obserwuje się parę wielkości fizycznych nazywanych w technice sygnałami.
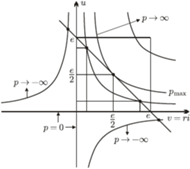
Rys. 2
Dla źródła energii elektrycznej parę sygnałów stanowią napięcie elektryczne i natężenie prądu elektrycznego, które oznaczymy 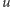 oraz
oraz 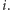 Iloczyn tych sygnałów stanowi moc chwilową:
Iloczyn tych sygnałów stanowi moc chwilową:

Na ogół zarówno 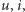 jak i
jak i 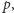 zależą od czasu, ale istnieje spora grupa źródeł energii, w których funkcje te są stałe w czasie (lub zmieniają się bardzo powoli) i dlatego nazywa się je źródłami napięcia (bądź prądu) stałego. Modele matematyczne takich źródeł są szczególnie proste, gdyż pomija się w nich zależność od czasu. Przykładami tego typu źródeł są ogniwa, prądnice prądu stałego, turbiny, ale również akumulatory samochodowe. Tymi ostatnimi zajmiemy się w tym artykule. Równanie opisujące akumulator, które wiąże ze sobą sygnały
zależą od czasu, ale istnieje spora grupa źródeł energii, w których funkcje te są stałe w czasie (lub zmieniają się bardzo powoli) i dlatego nazywa się je źródłami napięcia (bądź prądu) stałego. Modele matematyczne takich źródeł są szczególnie proste, gdyż pomija się w nich zależność od czasu. Przykładami tego typu źródeł są ogniwa, prądnice prądu stałego, turbiny, ale również akumulatory samochodowe. Tymi ostatnimi zajmiemy się w tym artykule. Równanie opisujące akumulator, które wiąże ze sobą sygnały  - napięcie oraz
- napięcie oraz 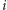 - natężenie prądu elektrycznego, ma postać
- natężenie prądu elektrycznego, ma postać

gdzie  nazywa się "siłą elektromotoryczną" źródła, natomiast
nazywa się "siłą elektromotoryczną" źródła, natomiast 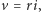 gdzie
gdzie  to tzw. opór wewnętrzny źródła. Równanie to na płaszczyźnie we współrzędnych
to tzw. opór wewnętrzny źródła. Równanie to na płaszczyźnie we współrzędnych 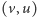 przedstawia prostą przechodzącą przez ćwiartki I, II i IV wyznaczoną przez punkty o współrzędnych
przedstawia prostą przechodzącą przez ćwiartki I, II i IV wyznaczoną przez punkty o współrzędnych 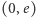 i
i 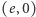 (Rys. 1). Pierwszy punkt nazywa się "punktem otwarcia" źródła - przy prądzie
(Rys. 1). Pierwszy punkt nazywa się "punktem otwarcia" źródła - przy prądzie 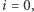 drugi punkt to tzw. "punkt zwarcia" - przy
drugi punkt to tzw. "punkt zwarcia" - przy 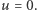 Napięcie elektryczne akumulatora przy
Napięcie elektryczne akumulatora przy 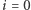 nazywa się napięciem otwarcia
nazywa się napięciem otwarcia 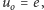 a prąd przy
a prąd przy 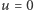 - prądem zwarcia
- prądem zwarcia 
Oprócz równania linii prostej we współrzędnych 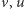 występuje jeszcze jedno równanie energetyczne:
występuje jeszcze jedno równanie energetyczne:

gdzie 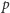 jest mocą wyprowadzaną z akumulatora. Jest to równanie hiperboli, która dla
jest mocą wyprowadzaną z akumulatora. Jest to równanie hiperboli, która dla 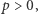 gdy akumulator się rozładowuje, przechodzi tylko przez ćwiartkę I, a dla
gdy akumulator się rozładowuje, przechodzi tylko przez ćwiartkę I, a dla 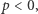 gdy akumulator się ładuje, przez ćwiartki II i IV. Hiperbola ma wówczas dwie gałęzie, jak to widać na wykresie.
gdy akumulator się ładuje, przez ćwiartki II i IV. Hiperbola ma wówczas dwie gałęzie, jak to widać na wykresie.
Wraz ze zmianą mocy 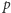 od
od 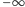 do
do 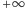 otrzymuje się całą rodzinę hiperbol. O tym, jaką wartość przyjmie moc
otrzymuje się całą rodzinę hiperbol. O tym, jaką wartość przyjmie moc 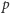 pobierana z akumulatora, decyduje czynnik zewnętrzny, czyli albo odbiornik energii, albo urządzenie ładujące źródło, przy czym własności akumulatora nakładają na możliwe wartości mocy pewne ograniczenia, których analizą się zajmiemy.
pobierana z akumulatora, decyduje czynnik zewnętrzny, czyli albo odbiornik energii, albo urządzenie ładujące źródło, przy czym własności akumulatora nakładają na możliwe wartości mocy pewne ograniczenia, których analizą się zajmiemy.
Rozpatrując proces pobierania energii z akumulatora, stawia się pytanie, kiedy moc 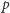 osiąga wartość maksimum. Poszukiwanie punktu maksimum
osiąga wartość maksimum. Poszukiwanie punktu maksimum 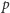 na wykresie polega na tym, aby spośród wszystkich prostokątów o bokach
na wykresie polega na tym, aby spośród wszystkich prostokątów o bokach 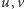 opierających się o prostą
opierających się o prostą 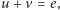 czyli o tym samym obwodzie, wybrać ten, który będzie miał największe pole powierzchni. Oczywiste jest, że prostokąt ten musi być kwadratem. Jest to równoważne z tym, że funkcja
czyli o tym samym obwodzie, wybrać ten, który będzie miał największe pole powierzchni. Oczywiste jest, że prostokąt ten musi być kwadratem. Jest to równoważne z tym, że funkcja

osiąga maksimum w punkcie 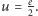 Punkt o współrzędnych
Punkt o współrzędnych

nazywa się punktem dopasowania odbiornika energii do źródła (akumulatora). Współrzędne tego punktu wyznaczają wartość mocy maksymalnej otrzymywanej z akumulatora

gdzie 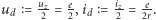 Zagadnienie dopasowania odbiorników do źródeł energii jest obszernym problemem technicznym i teoretycznym wymagającym zaangażowania bardziej rozwiniętego aparatu matematycznego (rachunek wariacyjny, analiza funkcjonalna). Ten problem znacznie się upraszcza i nazywa się dopasowaniem odbiornika do źródła napięcia stałego ze względu na maksimum pobieranej z niego mocy. W tym celu na rysunku 2 wyróżniamy dwa kwadraty: duży kwadrat, tzw. "otwarciowo-zwarciowy", o polu powierzchni
Zagadnienie dopasowania odbiorników do źródeł energii jest obszernym problemem technicznym i teoretycznym wymagającym zaangażowania bardziej rozwiniętego aparatu matematycznego (rachunek wariacyjny, analiza funkcjonalna). Ten problem znacznie się upraszcza i nazywa się dopasowaniem odbiornika do źródła napięcia stałego ze względu na maksimum pobieranej z niego mocy. W tym celu na rysunku 2 wyróżniamy dwa kwadraty: duży kwadrat, tzw. "otwarciowo-zwarciowy", o polu powierzchni 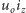 równym "mocy otwarciowo-zwarciowej" i mały kwadrat o polu powierzchni równym ćwiartce pola dużego kwadratu, a wynoszącym
równym "mocy otwarciowo-zwarciowej" i mały kwadrat o polu powierzchni równym ćwiartce pola dużego kwadratu, a wynoszącym 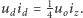 Ten mały można nazwać kwadratem mocy maksymalnej, ponieważ przez jeden z jego wierzchołków przechodzi hiperbola mocy maksymalnej styczna do prostej
Ten mały można nazwać kwadratem mocy maksymalnej, ponieważ przez jeden z jego wierzchołków przechodzi hiperbola mocy maksymalnej styczna do prostej 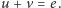 Położone wyżej hiperbole, odpowiadające mocom
Położone wyżej hiperbole, odpowiadające mocom 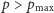 nie mają punktów wspólnych z prostą napięciowo-prądową źródła, co oznacza, że akumulator nie jest w stanie dostarczyć takiej mocy. Liczba 4 staje się tym samym w teorii źródeł energii liczbą "magiczną".
nie mają punktów wspólnych z prostą napięciowo-prądową źródła, co oznacza, że akumulator nie jest w stanie dostarczyć takiej mocy. Liczba 4 staje się tym samym w teorii źródeł energii liczbą "magiczną".
Punkty przecięć prostej 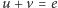 z hiperbolami rodziny
z hiperbolami rodziny 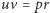 są punktami współpracy akumulatora z odbiornikiem bądź źródłem ładowania. Prosta przecina hiperbole w dwóch punktach w ćwiartkach II i IV (ładowanie akumulatora) albo w dwóch punktach w ćwiartce I (rozładowanie), albo w jednym punkcie (dopasowanie), albo ich nie przecina, gdy
są punktami współpracy akumulatora z odbiornikiem bądź źródłem ładowania. Prosta przecina hiperbole w dwóch punktach w ćwiartkach II i IV (ładowanie akumulatora) albo w dwóch punktach w ćwiartce I (rozładowanie), albo w jednym punkcie (dopasowanie), albo ich nie przecina, gdy 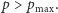 Ilustruje to rozwiązanie układu równań akumulatora
Ilustruje to rozwiązanie układu równań akumulatora 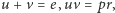 który sprowadza się do równania kwadratowego dla napięcia lub prądu:
który sprowadza się do równania kwadratowego dla napięcia lub prądu:

gdzie 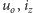 - wcześniej zdefiniowane napięcie otwarcia i prąd zwarcia akumulatora, a
- wcześniej zdefiniowane napięcie otwarcia i prąd zwarcia akumulatora, a

jest tzw. ułamkiem obciążenia źródła. Stosunek ten nie może przekroczyć wartości 1, gdyż w przeciwnym razie otrzymywalibyśmy z akumulatora więcej mocy, niż jest on w stanie dostarczyć. Matematycznie oznaczałoby to, że wyróżnik równań kwadratowych 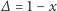 byłby ujemny i równania te nie miałyby rzeczywistych rozwiązań. Jednak dla ujemnych
byłby ujemny i równania te nie miałyby rzeczywistych rozwiązań. Jednak dla ujemnych  nie ma żadnego ograniczenia od dołu, może z wyjątkiem ograniczeń wynikających z wytrzymałości akumulatora na przeciążenie prądem lub napięciem. Ujemna wartość
nie ma żadnego ograniczenia od dołu, może z wyjątkiem ograniczeń wynikających z wytrzymałości akumulatora na przeciążenie prądem lub napięciem. Ujemna wartość 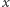 odpowiada procesowi ładowania akumulatora z zewnętrznego źródła energii elektrycznej.
odpowiada procesowi ładowania akumulatora z zewnętrznego źródła energii elektrycznej.
Przyjmijmy, że 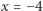 (magiczne minus 4) co oznacza, że akumulator ładowany jest z mocą równą polu powierzchni dużego kwadratu otwarciowo-zwarciowego. Wówczas równania kwadratowe przyjmą wspólną postać
(magiczne minus 4) co oznacza, że akumulator ładowany jest z mocą równą polu powierzchni dużego kwadratu otwarciowo-zwarciowego. Wówczas równania kwadratowe przyjmą wspólną postać

a to jest równanie złotego podziału! Jednym z rozwiązań tego równania jest liczba opisująca złoty podział ( 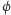 - symbol Fidiasza):
- symbol Fidiasza):

Drugim rozwiązaniem równania kwadratowego jest 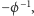 otrzymujemy więc dwa rozwiązania, którym odpowiadają następujące wartości prądu i napięcia:
otrzymujemy więc dwa rozwiązania, którym odpowiadają następujące wartości prądu i napięcia:

Punkty o tych współrzędnych leżą w ćwiartkach II i IV, co widać na rysunku 2 Korzystniejszą technicznie jest pierwsza para wartości ze względu na mniejszą wartość bezwzględną prądu ładowania (punkt w ćwiartce II). Zatem napięcie ładowania akumulatora  powinno być takie, aby
powinno być takie, aby 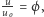 co przy
co przy 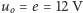 daje wartość około
daje wartość około 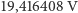 ( "złote napięcie ładowania"). Warto zauważyć, że prąd ładowania odpowiadający "złotemu napięciu" jest dosyć duży i wynosi
( "złote napięcie ładowania"). Warto zauważyć, że prąd ładowania odpowiadający "złotemu napięciu" jest dosyć duży i wynosi 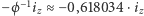 (
( 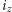 - prąd zwarcia). Nie jest to więc prąd mały, zważywszy, że prąd zwarcia płynący przez akumulator długotrwale może go uszkodzić. Badanie właściwości ładowania akumulatorów złotym napięciem bądź złotym prądem wymagałoby analizy wielu zjawisk fizykochemicznych, dynamicznych, cieplnych, itd. zachodzących w akumulatorze podczas ładowania. Autor w tym artykule nie podejmuje dyskusji na ten temat. Tutaj ograniczymy się do wyciągnięcia następującego wniosku sformułowanego w postaci twierdzenia:
- prąd zwarcia). Nie jest to więc prąd mały, zważywszy, że prąd zwarcia płynący przez akumulator długotrwale może go uszkodzić. Badanie właściwości ładowania akumulatorów złotym napięciem bądź złotym prądem wymagałoby analizy wielu zjawisk fizykochemicznych, dynamicznych, cieplnych, itd. zachodzących w akumulatorze podczas ładowania. Autor w tym artykule nie podejmuje dyskusji na ten temat. Tutaj ograniczymy się do wyciągnięcia następującego wniosku sformułowanego w postaci twierdzenia:
Twierdzenie. Napięcie (bądź prąd) ładowania akumulatora z mocą równą iloczynowi napięcia otwarcia i prądu zwarcia, równą czterokrotnej mocy maksymalnej - czyli równą polu powierzchni dużego kwadratu otwarciowo-zwarciowego - równe są 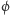 bądź
bądź 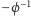 (złotej liczbie lub jej odwrotności) jednostek napięcia (lub prądu).
(złotej liczbie lub jej odwrotności) jednostek napięcia (lub prądu).