Na temat stabilności poruszającego się roweru napisano wiele artykułów, a nawet książek. Niestety, zagadnienie nie jest łatwe, większość artykułów upraszcza zagadnienie stabilności tak bardzo, że aż trudno określić, co jest prawdziwe, a co nie. Do sprawy stabilności roweru podejdziemy więc nieco inaczej, mianowicie od strony doświadczalnej. Fizyka jest nauką doświadczalną, bez względu na teorię dobrze jest zdawać sobie sprawę z tego, jak to jest w rzeczywistości.

Skoro zrozumienie stabilności roweru nie jest proste, posłużymy się starą metodą, żeby najpierw zrozumieć zagadnienie uproszczone. Tym uproszczonym zagadnieniem jest toczenie się koła rowerowego po płaszczyźnie. Doświadczenia z kołem rowerowym są łatwe do wykonania – wystarczy odkręcić koło od roweru. Jeśli koło postawimy w pozycji pionowej i przestaniemy je podtrzymywać, to koło prędko upadnie. Mówiąc inaczej, stojące w pozycji pionowej koło znajduje się w stanie równowagi nietrwałej. Spróbujmy jednak pchnąć to koło tak, by toczyło się po powierzchni. Nietrudno zauważyć, że koło będzie utrzymywać pozycję zbliżoną do pionu i będzie się toczyć bez upadku tak długo, aż jego prędkość zmaleje i koło straci równowagę. Toczące się koło zachowuje „samo z siebie” pozycję pionową; innymi słowy, pozycja pionowa toczącego się koła stanowi rodzaj trwałej równowagi, tak zwanej równowagi dynamicznej. Oczywiście, koło musi toczyć się dostatecznie szybko, aby ta równowaga wystąpiła.

Zastanówmy się, dlaczego tak się dzieje. Co stanie się z kołem, gdy z dowolnego powodu podczas toczenia przechyli się w lewo? Tor koła nie będzie już prostą, koło zacznie skręcać! Spróbujcie to sprawdzić, przechylenie koła powoduje jego skręt w stronę, w którą koło przechyliło się. To zjawisko można powiązać z efektem żyroskopowym. Na przechylone koło działają siła ciężkości oraz siła reakcji podłoża. Ta para sił daje moment sił skręcający koło w kierunku, w którym koło przechyliło się. Jednak ze względu na to, że koło się obraca, ten moment sił powoduje skręt koła w lewo. Zakrzywienie toru koła prowadzi do powstania siły odśrodkowej, a ta przeciwdziała dalszemu wychylaniu się. To właśnie siła odśrodkowa stabilizuje ruch i powoduje, że koło nie przewraca się.

Czytelnik Wnikliwy może się tu zastanawiać, czemu nie chcemy rozrysować działających sił i zastosować zasad dynamiki, przecież toczenie się koła po powierzchni można analizować podobnie jak analizuje się inne ruchy ciał. Toczenie się koła nie jest jednak prostym ruchem, występują tu więzy opisujące brak poślizgu. Koło toczy się bez poślizgu, ale, jak widzimy, wcale nie jest to ruch po prostej. Formalnie warunek toczenia się koła po płaszczyźnie prowadzi do tzw. więzów nieholonomicznych, analizowanych w uniwersyteckich podręcznikach mechaniki. Nie będziemy zajmować się więc teorią tego ruchu w odniesieniu do roweru, spróbujemy zrozumieć go na podstawie doświadczeń.

Rys. 1 Schemat roweru.

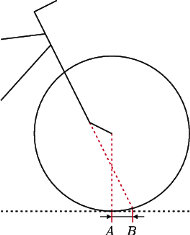
Rys. 2 Standardowa konstrukcja przedniego widelca. Przecięcie osi obrotu widelca z płaszczyzną podłoża (B) wyprzedza punkt styczności koła z podłożem (A) o kilka centymetrów.

Przyjrzyjmy się najpierw dobrze konstrukcji roweru (rysunek 1). Zauważmy, że oś przedniego widelca jest zawsze nachylona pod pewnym, na ogół niewielkim, kątem w stosunku do pionu. Ponadto przedłużenie osi przedniego widelca przebiega zawsze z tyłu za osią przedniego koła i dochodzi do ziemi w pobliżu punktu styczności przedniego koła z ziemią, wyprzedzając go o kilka centymetrów. Ilustruje to rysunek 2

Postawmy rower w standardowym położeniu, z ramą ustawioną pionowo i przednim kołem w płaszczyźnie ramy, jakbyśmy chcieli jechać do przodu. Rower prędko się przewróci, jeśli nie będziemy go podtrzymywać. Przechylajmy zatem rower powoli, trzymając go za siodełko, i zastanówmy się, co dzieje się z przednim kołem. Jeśli rower przechyli się na lewą stronę, to przednie koło skręci w lewo względem ramy. Oczywiście, przechylenie roweru w prawo powoduje podobne skręcenie przedniego koła, tyle że w prawo.

Jakie to ma znaczenie dla stabilności roweru? Jeśli rower jedzie po prostej, jego przednie koło znajduje się w płaszczyźnie ramy. Jeśli rower z jakiegoś powodu przechyli się, powiedzmy, na lewą stronę, to przednie koło skręci w lewo. Ruch roweru nie będzie odbywał się dalej po prostej, lecz po łuku. Powstanie więc siła odśrodkowa działająca na ramę roweru. Siła odśrodkowa skierowana będzie w prawo, pod jej wpływem rama roweru wyprostuje się, powróci do pionu. W ten sposób siła odśrodkowa stabilizuje rower w pozycji pionowej. Rzecz jasna, siła ta musi być dostatecznie duża, co oznacza, że rower musi jechać dostatecznie szybko. Warto zwrócić uwagę na fakt, że odchylanie koła w kierunku, w którym przechylił się rower, nie jest związane z efektem żyroskopowym, tylko z geometrią roweru i zachodzi nawet dla roweru w spoczynku. Efekt żyroskopowy oczywiście także występuje i w pewnym niewielkim stopniu przyczynia się do stabilności ruchu.

Spróbujmy potwierdzić opisany mechanizm zapewnienia stabilności. Zrobimy to metodą, którą można by nazwać metodą zaprzeczenia. Spróbujmy tak zmodyfikować konstrukcję roweru, aby rower stał się niestabilny. W tym celu należy tak zmienić układ kierowniczy, żeby zniwelować opisany wyżej mechanizm. Chodzi o to, by tak skonstruować montaż przedniego koła, aby przechylenie roweru w lewo powodowało skręcenie przedniego koła w prawo, czyli w stronę przeciwną do przechylenia roweru.

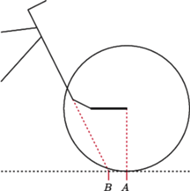
Rys. 3 Widelec przedłużony. Przecięcie osi obrotu widelca z płaszczyzną podłoża (B) znajduje się za punktem styczności koła z podłożem (A).

Spróbujmy przesunąć przednie koło roweru nieco bardziej do przodu. W tym celu należy zdjąć przednie koło, przykręcić dwa płaskowniki do widelca, a następnie przykręcić przednie koło do płaskowników, tak jak na rysunku 3 Długość płaskowników powinna wynosić co najmniej 20 cm. Należy zadbać o to, by koło było mocno dokręcone, a cała konstrukcja – sztywna. Spróbujcie teraz przechylić rower w lewą stronę. Przednie koło skręci w prawo!

Na takim rowerze na pewno nie da się jeździć. Każde przechylenie roweru w lewo powoduje skręt przedniego koła w prawo. Pojawi się więc siła odśrodkowa, która jeszcze bardziej będzie odchylać rower w lewą stronę. Upadku nie da się powstrzymać ruchami kierownicy ani poprzez przechylanie roweru w żadną stronę.

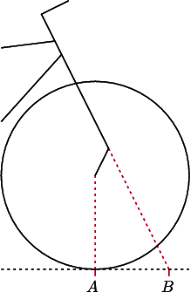
Rys. 4 Widelec obrócony w stronę ramy. Oś obrotu widelca przed osią przedniego koła, a punkt styczności koła z podłożem (A) przesunięty mocno do tyłu.

Zmodyfikujmy teraz rower w inny sposób, przesuwając przednie koło do tyłu. To może okazać się trudniejsze, gdyż między kołem a ramą może nie być dostatecznie dużo miejsca. Niektóre rowery mają jednak możliwość skręcenia kierownicy o 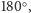  a po takim skręceniu widelec znajduje się w pozycji zilustrowanej na rysunku 4 Czy na takim rowerku daje się jechać?

Te negatywne doświadczenia mają za zadanie uzasadnienie, że stabilność roweru wynika z jego konstrukcji, a dokładniej sposobu zamontowania przedniego koła na widelcu.

Być może niektórzy z Czytelników widzieli rowery cyrkowe, służące do pokazywania różnych sztuczek. Te rowery mają inną konstrukcję: oś przedniego widelca jest pionowa i przechodzi przez środek przedniego koła. Taki rower nie wykazuje dużej stabilności, jednak cyrkowcy radzą sobie z tym dobrze.

Na koniec jeszcze jedna zagadka. Choć nie należy to do zabaw bezpiecznych, rowerem można próbować jechać nie tylko po drodze, ale też po poruszającej się taśmie używanej do biegania w siłowniach. Kiedy taśma się porusza, biegacz albo rowerzysta porusza się do przodu względem taśmy, ale pozostaje nieruchomy w układzie związanym z ziemią. Czyżby zatem w takim układzie nie występowała siła odśrodkowa stanowiąca zasadniczą przyczynę stabilności roweru? Czy więc rowerem nie da się jechać w miejscu po poruszającej się taśmie?