Otwieramy Internet, a tam na licznych forach krzyczą inne tytuły. Spójrzcie ludzie za okno, zimy coraz bardziej srogie, aktywność Słońca zanika, 24. cykl aktywności słonecznej będzie bardzo słaby, jesteśmy na progu zjawiska podobnego do minimum Maundera, czeka nas epoka lodowcowa, jakie już przecież kiedyś na Ziemi bywały.

Któremu stwierdzeniu uwierzyć? Przemysł, intensywne rolnictwo i hodowla rzeczywiście prowadzą do produkcji gazów cieplarnianych. Ale faktem jest też, że epoki lodowcowe na Ziemi się zdarzają. W ciągu ostatnich stu tysięcy lat było głównie zimno, z niewielkimi przerwami po parę tysięcy lat (zwanymi interglacjałami). Ciepło jest dopiero od dziesięciu tysięcy lat, a holocen to taki właśnie interglacjał. Ponadto, niezależnie od tego, czy jest ciepło czy zimno, występują spore wahania temperatury. Naukowcy nie rozumieją jeszcze w pełni tego zjawiska. Rozważane są różne hipotezy, a i dane obserwacyjne, którymi dysponujemy, nie są najlepsze. Precyzyjne pomiary wykonywane są przez stacje meteorologiczne od nieco ponad stu lat, a dokładniejsze globalne pomiary temperatury, obejmujące oceany, które przecież pokrywają ponad 70% powierzchni Ziemi, rozpoczęły się na dobre kilkanaście lat temu.

Mamy zatem do dyspozycji, przynajmniej dla ostatnich kilkunastu lat, zupełnie niezłe pomiary. I mamy to szczęście (albo nieszczęście), że w ostatnim czasie aktywność Słońca uległa niekwestionowanemu osłabieniu. Nasuwa się zatem pytanie, czy sprawcą zmian klimatu jest Słońce czy człowiek i w którą stronę ziemski klimat zmierza. Ponieważ otaczający nas zgiełk informacyjny utrudnia znalezienie jasnej odpowiedzi na te pytania, proponujemy Czytelnikom wykonywanie co jakiś czas, w miarę pojawiania się coraz nowszych i lepszych pomiarów, własnych obliczeń.

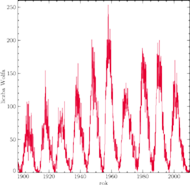
Rys. 1 Liczba Wolfa opisująca liczbę plam na Słońcu od roku 1900. Wyraźnie widać niemal cykliczną zmienność z okresem około 11 lat.

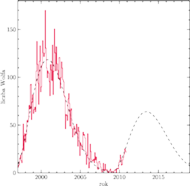
Rys. 2 Liczba Wolfa (linia ciągła) oraz jej przewidywana wartość (linia przerywana), otrzymana metodą opracowaną przez Hathawaya i współpracowników.

Osłabienie aktywności Słońca

Aktywność Słońca przejawia się w postaci częstego występowania plam słonecznych, rozbłysków, emisji rentgenowskiej i radiowej. Aktywność ta zmienia się prawie cyklicznie, z okresem około 11 lat. Aktywność w ciągu ostatnich 100 lat przedstawiona jest na rysunku 1. Oprócz zmian cyklicznych widać jednak także, że nie wszystkie maksima są jednakowo wysokie i nie wszystkie minima jednakowo długie. Ostatnie maksimum, przypadające na rok 2000, jest już niższe niż to poprzednie (z roku 1990), ostatnie minimum było wyjątkowo długie, a wszystko wskazuje na to, że najbliższe maksimum (spodziewane około roku 2013) będzie jeszcze niższe. Na rysunku 2 przedstawiony jest przewidywany i rzeczywisty przebieg wartości liczby plam na Słońcu według stanu na grudzień 2010. Zobaczymy, czy te przewidywania się potwierdzą.

W czasach historycznych było kilka epizodów zmniejszonej aktywności słonecznej. Najbardziej znane i nagłębsze to, zbiegające się z tzw. Małą Epoką Lodowcową, minimum Maundera w latach 1645–1717, kiedy to plamy słoneczne niemal nie występowały. Nie tak już głębokie było minimum Daltona w latach 1790–1830, w środku którego miała miejsce wyprawa Napoleona na Rosję, zakończona porażką m.in. z powodu ciężkiej zimy. Można sądzić, że osłabienie aktywności Słońca skutkuje spadkiem temperatury na Ziemi.

Pomiary emisyjności Słońca potwierdziły pewien związek – gdy Słońce jest aktywne, emituje więcej energii – ale ta zmiana jest zaledwie rzędu 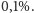 Modele klimatu Ziemi nie przewidują, żeby tak mała zmiana przekładała się na znaczącą zmianę temperatury. Obliczenia wskazują zmiany rzędu 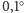C. Są jednak sugestie, że mogą działać także pewne sprzężenia zwrotne, związane ze zmianami w wietrze słonecznym oraz promieniowaniu kosmicznym. Mianowicie, słaby wiatr słoneczny nie chroni nas przed cząstkami promieniowania kosmicznego, które mogą mieć wpływ na formowanie się pewnego typu chmur w górnych warstwach atmosfery, to zaś może wpływać na osłabienie światła słonecznego. Nie ma jednak dobrego modelu tego zjawiska.

Opisane wyżej niepewności skłaniają nas do możliwie ostrożnego formułowania hipotez. Przyjmiemy zatem, że niewykluczone jest, iż aktywność Słońca wpływa na ziemski klimat, a zatem zmiany klimatu mogą odzwierciedlać zmiany aktywności Słońca.

Zmiany temperatury na Ziemi

Zajmijmy się zatem problemem temperatury: rośnie czy nie? Średnią roczną wartość odchylenia temperatury na powierzchni Ziemi (od roku 1880 do dziś) znaleźć można w bazie GISTEMP. Dane te opierają się na pomiarach z meteorologicznych stacji naziemnych oraz pomiarach satelitarnych. Pomiary ze stacji naziemnych są starannie selekcjonowane (na podstawie obserwacji satelitarnych) w celu uniknięcia błędów związanych ze zjawiskiem miejskich „wysp ciepła”. Pomiary temperatury powierzchni wody w oceanach pochodzą z obserwacji satelitarnych, zbieranych przez National Oceanic and Atmospheric Administration (tzw. baza OISST.v2). Włączone tam są także pomiary na Antarktydzie, podawane co miesiąc przez Scientific Committee on Antarctic Research. Sposób opracowywania danych opisany jest szczegółowo w pracy opublikowanej w grudniu 2010 r.. Podane wartości obejmują zatem zarówno powierzchnię lądów, jak i oceanów. Uwzględnienie oceanów jest niezwykle ważne, ponieważ lądy stanowią mniej niż 30% powierzchni Ziemi, a w dodatku woda ma znacznie większą bezwładność cieplną i w mniejszym stopniu wykazuje wahania chwilowe, a w większym akumulujące się trendy. Opisywana baza podaje anomalię (różnicę temperatury), a nie samą wartość, ponieważ pomiar taki jest obarczony mniejszym błędem. Okresem odniesienia w tej bazie jest okres lat 1951–1980. W chwili pisania artykułu nie ma tam jeszcze pełnych danych za rok 2010, ale są dane do listopada włącznie, więc można uśrednić dane od stycznia do listopada i uznać to za dobre przybliżenie. Czytelnikom radzimy skorzystać z nowszych danych.

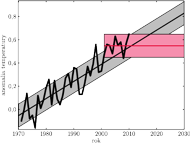
Rys. 3 Wykres obserwowanego przebiegu anomalii temperatury (linia gruba łamana), dopasowanie trendu wznoszącego (linia czarna) oraz stałej wartości od roku 2001 (linia czerwona). Obszar zacieniowany to otrzymany zakres błędów (fluktuacji krótkookresowych).

Dane zawarte w opisanej wyżej bazie pozwalają nam analizować zmiany temperatury w ciągu ostatnich dekad. Skupimy się tutaj na okresie od 1970 roku do chwili obecnej. Wykres, przedstawiony na rysunku 3, pozwala stwierdzić, że, ogólnie rzecz biorąc, temperatura rośnie, choć ostatnio jakoś mniej (szczególnie jeśli nie patrzeć na ostatni analizowany rok, czyli 2010). Podzielimy zatem dane na dwie grupy: okres 1970–2000 i okres 2001–2010. W tym pierwszym okresie temperatura niewątpliwie rośnie. Jest to zgodne z odczuciem jednego z autorów, pamiętającego z dzieciństwa (lata 60. XX w.) corocznie śnieżne zimy, w odróżnieniu od lat późniejszych. Ten wzrost możemy scharakteryzować ilościowo, dopasowując do trendu wzrostowego linię prostą. Metody statystyczne podpowiadają nam, że jest na to prosty przepis.

Prosta analiza statystyczna

Powiedzmy, że mamy zbiór pomiarów temperatury 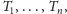 wykonanych w chwilach 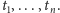 Szukamy takiej prostej 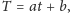 która możliwie najlepiej opisuje trend pomiarowy. W tym celu określamy funkcję:

Wyrażenie w licznikach to kwadrat różnicy między dopasowywaną prostą a prawdziwą wartością pomiaru w danej chwili 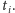 Wyrażenia w mianowniku to kwadraty błędów pomiarowych. Tak zdefiniowana funkcja nawiązuje do pewnej koncepcji, niezwykle ważnej w statystyce. Załóżmy, że mamy ciąg  niezależnych zmiennych losowych, każda o standardowym rozkładzie normalnym o średniej zero i dyspersji 1. Wtedy zmienna losowa będąca sumą ich kwadratów ma rozkład 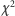 o  stopniach swobody.

Istnieje wiele ważnych twierdzeń na temat własności tego rozkładu, a niektóre pożyteczne własności są stablicowane. My jednak do skomplikowanych twierdzeń tu odwoływać się nie będziemy, a nasze dalsze rozważania będą mieć charakter intuicyjny i jakościowy.

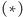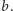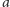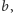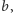Funkcja  zależy od dwóch nieznanych parametrów rzeczywistych  i  Jest ona sumą wyrazów dodatnich, tym mniejszych, im lepiej nasza funkcja opisuje prawdziwy przebieg temperatury. Możemy to wykorzystać do obliczenia  i  zakładając, że najlepiej opisują rzeczywistość te wartości parametrów, dla których funkcja przyjmuje wartość najmniejszą. Ponieważ jest to funkcja kwadratowa  i  wyznaczenie jej minimum nie powinno nastręczać zbytnich trudności.

No właśnie, nie powinno, gdybyśmy znali wartości błędów pomiarowych. Tak jednak nie jest. Załóżmy zatem dla uproszczenia, że wszystkie są jednakowe (pomiary były wykonywane tą samą metodą za pomocą takich samych urządzeń). Położenie minimum funkcji 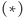 nie zależy wtedy od wartości błędu pomiarowego. Wykonując obliczenia dla lat 1970–2000 (31 punktów pomiarowych), uzyskujemy 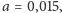 co oznacza, że przy najlepszym dopasowaniu temperatura rośnie o 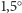C na stulecie. Wartość 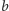 nie jest istotna z punktu widzenia kierunku trendu. Uzyskana w ten sposób prosta jest zaznaczona kolorem czarnym na rysunku 3, gdzie wykonano także ekstrapolację (czyli przedłużenie) trendu dla lat 2000–2010. Punkty pomiarowe dla lat 2000–2010 nie odstają zbytnio od tej prostej. W oparciu o nasze wcześniejsze rozważania, dotyczące związku klimatu z aktywnością Słońca, możemy jednak także założyć, że od roku 2000 temperatura już nie rośnie. W takim przypadku dobry opis punktów pomiarowych powinna zapewniać prosta pozioma odpowiadająca średniej wartości anomalii temperatury z lat 2001–2010. Zaznaczamy ją na wykresie kolorem. Patrząc na obie proste – tę wznoszącą się i tę poziomą – trudno powiedzieć, która jest lepszym opisem danych z ostatniej dekady.

Prawda a statystyka

Metody statystyczne pozwalają na rozstrzygnięcie tego problemu, wymagają one wszakże dokładnej znajomości błędów występujących w równaniu 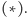 Nie ma ich jednak w żadnej tabeli. Musimy się więc odwołać do metod z pogranicza fizyki i sztuki. Dane z okresu 1970–2000 wydają się „na oko” zgodne z liniowym trendem wznoszącym. A zatem dla tych danych pomiary nie powinny odstawać od rzeczywistego trendu więcej niż o wartość błędu pomiarowego 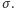 Z kolei różnica dużo mniejsza niż 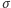 jest mało prawdopodobna z uwagi na nieunikniony rozrzut w wyniku błędów pomiaru. Oznacza to, że dla najlepszego dopasowania wartość tej funkcji 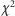 powinna wynosić w przybliżeniu tyle, ile mamy pomiarów, czyli 31. Znając wartośc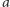i  i 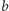 oraz podstawiając 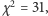 możemy wyznaczyć wartość 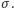 W naszym przypadku 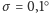C. To określenie błędu pozwala nam narysować wokół trendów pas niepewności wynikający z krótkoskalowych fluktuacji. Pas taki dodany do trendu wzrostowego pokazuje, że pomiary z okresu 2001–2010 dobrze mieszczą się w przewidzianym trendzie. Ale taki sam pas dodany do trendu poziomego (zaznaczony kolorem na rysunku 3) też dobrze opisuje sytuację, a oba pasy niemal się pokrywają dla rozważanego okresu. Czyli na pytanie, czy temperatura rośnie, czy nie rośnie, odpowiedź mamy taką: temperatura rośnie albo i nie rośnie... Niestety, obecny okres pomiarowy jest za krótki, aby coś stwierdzić, i nic na to nie można poradzić. Musimy więc czekać. Jak długo?

To można ocenić, ekstrapolując oba trendy na następne 20 lat. Przez następnych kilka lat pasy niepewności wokół obu prostych będą na siebie zachodziły, co oznacza, że nie da się rozróżnić dwóch hipotez. Ale za 20 lat różnice będą już wyraźne. Młodzi Czytelnicy pomyślą sobie, że taki szmat czasu to w zasadzie wieczność, ale w nauce czas potrafi płynąć bardzo powoli. Trzeba po prostu uzbroić się w cierpliwość. W jej braku można spróbować łączyć pomiary (użyć średniej z dwóch-trzech lat) i powtórzyć tę samą analizę. To może zmniejszyć trochę fluktuacje i ewentualnie skrócić nieco czas czekania na odpowiedź. Ćwiczenie to pozostawiamy do wykonania Czytelnikom.