Co to jest?
Jak to działa?
Komputery kwantowe
Wszyscy wiemy, że wiele problemów nie daje się rozwiązać za pomocą komputera tylko z powodu ich zbyt dużej „złożoności obliczeniowej”. Pod tym poważnym stwierdzeniem kryje się prosta i smutna prawda. Nawet najszybsze komputery są zbyt wolne, aby uporać się z niejednym zadaniem. Wiemy też, że nie da się w nieskończoność zwiększać szybkości komputerów. Rozmiary atomów wyznaczają możliwą do wyobrażenia skalę miniaturyzacji. Jako że żaden sygnał nie może rozchodzić się szybciej niż światło w próżni, czas potrzebny na przesłanie informacji między fragmentami procesora też jest ograniczony od dołu. Czy komputer kwantowy może stać się remedium na powyższy problem?
Pierwszy raz z nazwą „komputer kwantowy” zetknąłem się 9 lat temu, na
pierwszym roku studiów. Wydała mi się nieco podejrzana. Przecież zasada
nieoznaczoności Heisenberga wyklucza dokładne pomiary obiektów
kwantowych, powinna więc uniemożliwiać działanie takiego urządzenia. Tak
naprawdę to wymienione ograniczenia są, obok gwałtownie rosnącego zużycia
energii, główną przeszkodą przy tworzeniu coraz mniejszych i szybszych
komputerów „klasycznych”. Celowo użyłem cudzysłowu, bowiem w obecnie
produkowanych procesorach prawa mechaniki kwantowej odgrywają
już znaczącą rolę – tak naprawdę trudno opisać klasycznie działanie
pojedynczego tranzystora
 Na czym więc ma polegać owa
kwantowość? Na zupełnie odmiennym sposobie przetwarzania informacji.
We współczesnych komputerach informacja jest zapamiętywana jako ciąg
bitów, czyli zer i jedynek. Obliczenia zatem sprowadzają się do odpowiedniego
zamieniania jednych bitów na inne.
Na czym więc ma polegać owa
kwantowość? Na zupełnie odmiennym sposobie przetwarzania informacji.
We współczesnych komputerach informacja jest zapamiętywana jako ciąg
bitów, czyli zer i jedynek. Obliczenia zatem sprowadzają się do odpowiedniego
zamieniania jednych bitów na inne.
W komputerze kwantowym bity są zastąpione przez qubity (quantum bits).
Każdy qubit
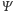 może być w tak zwanej superpozycji pomiędzy zerem
i jedynką. Zapisujemy to w ten sposób:
może być w tak zwanej superpozycji pomiędzy zerem
i jedynką. Zapisujemy to w ten sposób:
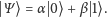
Jeśli dokonamy pomiaru wartości qubitu, to możemy otrzymać
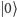 lub
lub
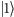 z prawdopodobieństwami równymi odpowiednio:
z prawdopodobieństwami równymi odpowiednio:
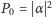 oraz
oraz
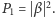 Przykładem tu może być elektron
ze spinem skierowanym w górę lub w dół.
Przykładem tu może być elektron
ze spinem skierowanym w górę lub w dół.
Takie uogólnienie bitu można jednak osiągnąć klasycznie. Wystarczy
zbudować klasyczny komputer analogowy. Każdy bit będzie przybierał
wartości z przedziału
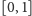 i gotowe.
i gotowe.
Nie chodzi jednak o operowanie wartościami między 0 i 1, lecz o wykorzystanie praw mechaniki kwantowej, pozwalających na superpozycję stanów jednego lub więcej qubitów.
Zobaczmy, jak to wygląda na przykładzie dwóch qubitów. Najprostsza baza układu
dwóch qubitów to oczywiście:
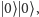
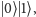
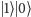 oraz
oraz
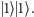 Przykładowy stan to pewna kombinacja liniowa wektorów bazy;
np.
Przykładowy stan to pewna kombinacja liniowa wektorów bazy;
np.
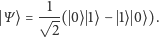
Pierwszy qubit może być zerem lub jedynką. Obie możliwości są jednakowo prawdopodobne. Drugi tak samo. Wiemy jednak, że zawsze będą miały przeciwne wartości. Zaczyna robić się ciekawie, ale po chwili zastanowienia możemy zaproponować klasyczny odpowiednik tej sytuacji. Weźmy dwie kule: białą i czarną. Włóżmy je, nie patrząc, do dwóch kieszeni. Nie wiemy jednak, gdzie znajduje się któraś z nich, ale wiemy, że kule w kieszeniach są różne.
Aby pokazać różnicę między mechaniką kwantową a klasyczną statystyką,
zamienię oznaczenia. Zamiast
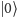 będę pisał
będę pisał
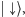 natomiast
natomiast
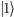 zastąpię przez
zastąpię przez
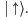 Wprowadzę również dwa nowe stany,
będące superpozycjami powyższych:
Wprowadzę również dwa nowe stany,
będące superpozycjami powyższych:
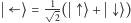 oraz
oraz
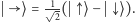 Są to stany spinu skierowanego odpowiednio
w lewo i prawo. Prosty rachunek (zachęcam!) pokazuje:
Są to stany spinu skierowanego odpowiednio
w lewo i prawo. Prosty rachunek (zachęcam!) pokazuje:
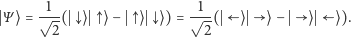
Wynik jest dość dziwny. Wygląda bowiem na to, że elektrony „nie wiedzą”, czy zostały „złożone” z elektronów o spinach góra-dół, czy też lewo-prawo. Co gorsza, my też tego nie wiemy! To tak, jakbyśmy po sprawdzeniu, że kulka z lewej kieszeni jest czerwona, wiedzieli, że ta z prawej jest zielona. Co więcej, moglibyśmy wybrać dowolną parę kolorów dopełniających. Jest tylko jedno ograniczenie: takiego „magicznego” pomiaru możemy dokonać tylko raz. Po pierwszym pomiarze owo połączenie czy też „splątanie” – jak mawiają fizycy – pomiędzy elektronami znika. Każdy z nich ma już określony stan.
Owa przedziwna własność stanów splątanych jest kluczowa – jest tym, co naprawdę odróżnia komputer kwantowy od klasycznego. Aby ją lepiej zrozumieć, musimy najpierw dowiedzieć się, na czym polega pomiar w mechanice kwantowej.
Nie możemy „zapytać”, jak skierowany jest spin elektronu. Możemy
spytać się jedynie, czy jest skierowany w górę czy w dół. Możemy także
wybrać inny pomiar: w lewo czy w prawo albo w przód czy w tył. Ale nie
możemy zadać tych pytań naraz. Tego typu zakazy wynikają z zasady
nieoznaczoności. Ograniczenie powyższe nie wynika z niedoskonałości
przyrządów pomiarowych. Popatrzmy na definicję spinów skierowanych
w bok. Widać, że elektron o spinie skierowanym w prawo niejako składa się
z elektronów o spinach skierowanych w górę i w dół. Zatem jeśli mamy
przyrząd, który rozróżnia elektrony
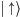 od
od
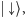 to elektron
to elektron
 „musi się zdecydować” na jedną z tych możliwości. Nie mamy
i mieć nie możemy na to wpływu. Każde urządzenie, które wykrywa
wszystkie elektrony
„musi się zdecydować” na jedną z tych możliwości. Nie mamy
i mieć nie możemy na to wpływu. Każde urządzenie, które wykrywa
wszystkie elektrony
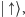 musi wykryć co najmniej połowę elektronów
musi wykryć co najmniej połowę elektronów
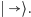 To, czy wykryje połowę czy więcej, zależy tylko od tego, jak reaguje
na elektrony
To, czy wykryje połowę czy więcej, zależy tylko od tego, jak reaguje
na elektrony
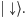
Budując algorytmy kwantowe, mamy do dyspozycji dodatkowe stany. Wydawać by się mogło, że z łatwością powinno dać się skonstruować mnóstwo algorytmów znacznie efektywniejszych niż klasyczne. Problemem jest jednak brak możliwości rozróżniania dowolnych stanów. Co z tego, że otrzymamy wspaniały rezultat, jeśli nie będziemy go w stanie odczytać. Dlatego obecnie znamy tak naprawdę tylko dwa algorytmy kwantowe.
Pierwszym jest algorytm Shora. Nie będę tutaj tłumaczył całego algorytmu, gdyż jego opis jest długi i raczej żmudny. Pozwala on rozłożyć liczbę na czynniki pierwsze. Jak wiadomo, jest to kluczowy element łamania tak zwanych szyfrów z kluczem publicznym RSA (używanych powszechnie do szyfrowania informacji w Internecie, np. przez banki). Nie ma wątpliwości, że to jedna z ważniejszych przyczyn zainteresowania informatyką kwantową.
W algorytmie zaproponowanym przez Shora najpierw sprowadza się problem
rozłożenia liczby
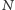 na czynniki pierwsze do problemu znalezienia
okresu pewnej funkcji. Jest ona zadana dla
na czynniki pierwsze do problemu znalezienia
okresu pewnej funkcji. Jest ona zadana dla
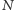 wartości. Procedura ta jest
w pełni klasyczna – pomijam ją tutaj. Po szczegóły odsyłam do oryginalnej
pracy [1]. Standardową metodą znajdywania okresu funkcji jest obliczenie jej
transformaty Fouriera. W wyniku tej operacji znajdujemy tak zwane widmo.
Gdyby funkcja opisywała falę dźwiękową, to dzięki transformacji Fouriera
dostalibyśmy informację, jakie tony zawiera dźwięk. Podobnie, dla światła,
byłby to rozkład na fale płaskie o określonych częstościach (czyli barwach).
Transformacja Fouriera pozwala po prostu wyrazić funkcję przez szereg
sinusów i kosinusów o różnych okresach. W wyniku transformacji
funkcji, określonej dla
wartości. Procedura ta jest
w pełni klasyczna – pomijam ją tutaj. Po szczegóły odsyłam do oryginalnej
pracy [1]. Standardową metodą znajdywania okresu funkcji jest obliczenie jej
transformaty Fouriera. W wyniku tej operacji znajdujemy tak zwane widmo.
Gdyby funkcja opisywała falę dźwiękową, to dzięki transformacji Fouriera
dostalibyśmy informację, jakie tony zawiera dźwięk. Podobnie, dla światła,
byłby to rozkład na fale płaskie o określonych częstościach (czyli barwach).
Transformacja Fouriera pozwala po prostu wyrazić funkcję przez szereg
sinusów i kosinusów o różnych okresach. W wyniku transformacji
funkcji, określonej dla
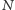 punktów, dostajemy funkcję (również
punktów, dostajemy funkcję (również
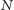 -punktową), której każdy punkt dostarcza informacji, „ile jest danej
częstości”.
-punktową), której każdy punkt dostarcza informacji, „ile jest danej
częstości”.
I tak oto dostajemy wynik – rozkład liczby na czynniki pierwsze. Zaniepokoić
powinny nas dwie rzeczy. Po pierwsze, transformatę Fouriera umiemy obliczać
klasycznie – gdzie więc jest mechanika kwantowa? Po drugie, czas potrzebny
na jej obliczenie jest proporcjonalny do
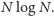 Widać więc, że jest to
fatalny algorytm. Najprostszy pomysł na rozłożenie
Widać więc, że jest to
fatalny algorytm. Najprostszy pomysł na rozłożenie
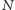 to sprawdzać
wszystkie liczby od
to sprawdzać
wszystkie liczby od
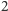 do
do
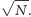 Rzecz w tym, że transformatę
Fouriera można obliczyć bardzo szybko kwantowo. Realizuje to odpowiedni
układ „bramek kwantowych”, czyli po prostu można wykonać stosowne
obliczenia za pomocą manipulacji na spinach elektronów. Jak każde rachunki,
można je przeprowadzić na różne sposoby. Jednak niezależnie od tego, jak
byśmy się starali, zawsze musimy uwzględnić operacje „splątujące”, a więc
takie, które z dwóch nieskorelowanych elektronów zrobią splątaną parę.
Stanowi to ogromną trudność eksperymentalną.
Rzecz w tym, że transformatę
Fouriera można obliczyć bardzo szybko kwantowo. Realizuje to odpowiedni
układ „bramek kwantowych”, czyli po prostu można wykonać stosowne
obliczenia za pomocą manipulacji na spinach elektronów. Jak każde rachunki,
można je przeprowadzić na różne sposoby. Jednak niezależnie od tego, jak
byśmy się starali, zawsze musimy uwzględnić operacje „splątujące”, a więc
takie, które z dwóch nieskorelowanych elektronów zrobią splątaną parę.
Stanowi to ogromną trudność eksperymentalną.
A jak duży musi być komputer kwantowy, aby poradzić sobie
z rozkładem liczby
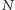 ? Przede wszystkim liczba ta musi zmieścić się
w jego „pamięci”. Oznacza to, że
? Przede wszystkim liczba ta musi zmieścić się
w jego „pamięci”. Oznacza to, że
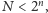 gdzie
gdzie
 jest właśnie
liczbą qubitów. To bardzo ważne, bowiem w wielu przypadkach obowiązuje
„zasada zachowania trudności”: zwiększenie szybkości algorytmu osiągane jest
za cenę większej „pamięciożerności”.
jest właśnie
liczbą qubitów. To bardzo ważne, bowiem w wielu przypadkach obowiązuje
„zasada zachowania trudności”: zwiększenie szybkości algorytmu osiągane jest
za cenę większej „pamięciożerności”.
Rzeczywiście, transformację Fouriera możemy wykonać bardzo łatwo, kodując funkcję za pomocą fali elektromagnetycznej, a widmo uzyskać natychmiast, przepuszczając światło przez pryzmat lub siatkę dyfrakcyjną. Problemem jest tu jednak ogromna liczba częstości, jakie musielibyśmy rozróżniać. Liczby pierwsze stosowane w kryptografii mają często po kilkaset cyfr. Nie ma najmniejszych szans na rozróżnianie częstości światła z tak ogromną precyzją. W algorytmach klasycznych czas potrzebny na rozłożenie liczby rośnie wykładniczo z liczbą jej cyfr (jej logarytmem). Przy zastosowaniu algorytmu Shora i optyki klasycznej wykładniczo rośnie liczba potrzebnych częstości światła. W algorytmie kwantowym, dzięki splątaniu, czas obliczeń i ilość qubitów rosną potęgowo wraz z logarytmem rozkładanej liczby.
Widać więc, że algorytm Shora to w zasadzie szukanie okresu funkcji. Nie jest to raczej problem fascynujący sam w sobie. Zawdzięcza on swoją popularność temu, że Shor potrafił powiązać ten pozornie czysto akademicki problem z kryptografią. To uczy, że bardzo ryzykowne jest „spisywanie na straty” jakiegoś działu nauki, mówiąc, że „to się do niczego nie przyda”.
Na koniec jedna uwaga. Dlaczego upieram się, że komputer kwantowy ma szukać okresu funkcji, a nie po prostu obliczyć transformatę Fouriera? Ten ostatni problem jest ważny w niezliczonych zastosowaniach. Od diagnostyki medycznej, poprzez analizę zdjęć satelitarnych, na symulacjach układów chemicznych kończąc. Otóż komputer kwantowy potrafi obliczyć transformatę Fouriera zawsze, ale wynik możemy odczytać tylko jeśli funkcja jest okresowa. Powód jest prosty: tylko dla funkcji okresowej widmo zawiera niewiele częstości. Jeśli będziemy próbować obliczać transformatę Fouriera z funkcji nieokresowej, to otrzymamy widmo złożone z niezliczonej ilości długości fal. A podczas pomiaru możemy dostać tylko jedną wartość częstości... Drugim zaproponowanym algorytmem kwantowym [2] jest sposób przeszukania zbioru N-elementowego w poszukiwaniu jednego „dobrego” elementu. W wielu przypadkach jest tak, że łatwo sprawdzić, czy zaproponowane rozwiązanie jest dobre. Trudno je jednak znaleźć. Często pozostaje nam jedynie sprawdzanie po kolei wszystkich możliwych przypadków. Kłopot zaczyna się, gdy jest ich dużo.
Klasyczny średni czas szukania jednego „dobrego” elementu spośród
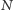 jest proporcjonalny do
jest proporcjonalny do
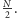 Czas potrzebny dla komputera
kwantowego to tylko
Czas potrzebny dla komputera
kwantowego to tylko
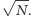 Wszystkie
Wszystkie
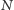 sprawdzanych
odpowiedzi możemy ponumerować. Od tej pory będziemy sprawdzać,
która z
sprawdzanych
odpowiedzi możemy ponumerować. Od tej pory będziemy sprawdzać,
która z
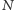 liczb jest „dobra”.
liczb jest „dobra”.
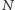 liczb zakodujemy za pomocą
liczb zakodujemy za pomocą
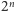 qubitów. Pokażę to na prostym przykładzie
qubitów. Pokażę to na prostym przykładzie
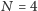 (
(
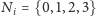 ):
):
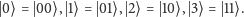
Kodowanie jest więc takie, jak w komputerze klasycznym. Następnie tworzymy stan będący superpozycją wszystkich możliwych odpowiedzi:
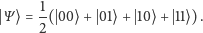
Zwracam uwagę, że jest to stan bardzo silnie splątany. Sprawdzanie, czy dana
liczba jest dobra, można zdefiniować jako obliczenie funkcji. Jeśli liczba jest
dobra, to funkcja ma wartość
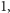 a jeśli zła, to
a jeśli zła, to
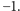 Oczywiście,
możemy przypisać inne wartości obu odpowiedziom – byleby tylko były
różne.
Oczywiście,
możemy przypisać inne wartości obu odpowiedziom – byleby tylko były
różne.
Widać więc, że wszystkie
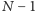 złych stanów będzie zawsze
traktowane tak samo, a inaczej jeden stan dobry. Możemy więc ogólnie
zapisać
złych stanów będzie zawsze
traktowane tak samo, a inaczej jeden stan dobry. Możemy więc ogólnie
zapisać
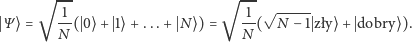
Jak widać, jeśli zmierzymy, w którym stanie jest układ
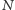 qubitów, to
z prawdopodobieństwem
qubitów, to
z prawdopodobieństwem
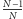 dostaniemy „złą” odpowiedź, a „dobrą”
jedynie z prawdopodobieństwem
dostaniemy „złą” odpowiedź, a „dobrą”
jedynie z prawdopodobieństwem
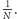 Jest to dość oczywiste – nic
jeszcze nie zrobiliśmy i szansa wylosowania stanu o szukanym numerze jest
znikoma.
Jest to dość oczywiste – nic
jeszcze nie zrobiliśmy i szansa wylosowania stanu o szukanym numerze jest
znikoma.
Zwróćmy uwagę, że otrzymany stan jest nieco podobny do pojedynczego spinu. Jeśli przyjmiemy

to otrzymamy:
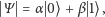
a więc spin skierowany prawie idealnie do dołu. Spin możemy obrócić o 180 stopni i dostaniemy elektron o spinie skierowanym niemal idealnie do góry. Obrotu pojedynczego spinu można dokonać, np. włączając jednorodne pole magnetyczne lub pole magnetyczne połączone z falą elektromagnetyczną. Jest to technika powszechnie stosowana w obrazowaniu i spektroskopii, opartych na zjawisku rezonansu magnetycznego (zazwyczaj spiny pochodzą tam od jąder, a nie od elektronów – jest to dla nas bez znaczenia. Elektron jest tylko przykładem cząstki ze spinem. Do budowy komputera można użyć innych cząstek).
Oczywiście, w przypadku układu
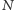 spinów nie jest tak prosto. Co
więcej, problemem jest to, że nie znamy dokładnie stanu
spinów nie jest tak prosto. Co
więcej, problemem jest to, że nie znamy dokładnie stanu
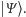 Po prostu
nie wiemy, co oznacza
Po prostu
nie wiemy, co oznacza
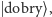 gdyż to jest nasza niewiadoma. Ale
znamy nasz stan z bardzo dobrym przybliżeniem, dlatego też możemy
z niezłym przybliżeniem go „obrócić”. Zajmuje to
gdyż to jest nasza niewiadoma. Ale
znamy nasz stan z bardzo dobrym przybliżeniem, dlatego też możemy
z niezłym przybliżeniem go „obrócić”. Zajmuje to
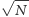 kroków.
Niestety, nie możemy obrócić układu w jednym kroku. Musimy „drobić”, bo
gdybyśmy „robili zbyt duże kroki”, moglibyśmy pójść nieco za daleko. To
cena, jaką płacimy za niedokładną znajomość stanu początkowego.
kroków.
Niestety, nie możemy obrócić układu w jednym kroku. Musimy „drobić”, bo
gdybyśmy „robili zbyt duże kroki”, moglibyśmy pójść nieco za daleko. To
cena, jaką płacimy za niedokładną znajomość stanu początkowego.
Niestety, pomimo ogromnego wysiłku, nie udało się dotąd zbudować działającego komputera kwantowego i nie wiadomo, czy będzie to kiedykolwiek możliwe. Jak już wspomniałem, nie musimy koniecznie używać elektronów. Próbowano rozmaitych schematów, w tym jądrowego rezonansu magnetycznego.
W tej chwili najbardziej obiecujące wydają się próby z jonami umieszczonymi w pułapce [3, 4]. Można już w sposób kontrolowany umieścić jeden za drugim kilka jonów w próżni. Ich pozycja jest kontrolowana za pomocą odpowiednio uformowanego pola elektromagnetycznego. Co więcej, możliwe jest dokonywanie manipulacji na wybranym jonie oraz ich splątywanie! Niestety, problemem jest tak zwana dekoherencja: po czasach rzędu milisekund w niezwykle przecież delikatny układ wkrada się jakieś zaburzenie. Powoduje to utratę informacji. Nie wiadomo, czy kiedykolwiek uporamy się praktycznie z tym problemem. Wraz ze wzrostem komputera, problem będzie się nasilał. Już jednak zbudowanie układu kilku qubitów i precyzyjna nimi manipulacja pokazuje, jak niesamowity rozwój technik eksperymentalnych nastąpił w ostatnich latach.
Z pewnością komputer kwantowy nie będzie kolejną zabawką stojącą na biurku, lecz urządzeniem służącym do wykonywania najbardziej zaawansowanych obliczeń, umieszczonym w najlepszych światowych laboratoriach. Trzeba jednak pamiętać, że taką samą przyszłość wieszczono klasycznym komputerom...