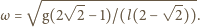Klub 44F - zadania V 2017»Zadanie 638
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania V 2017
- Publikacja w Delcie: maj 2017
- Publikacja elektroniczna: 1 maja 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (104 KB)
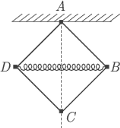
Układ składa się z czterech jednakowych, lekkich prętów o długości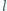 
i lekkiej sprężyny o długości 
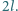Pręty połączone są przegubowo za pomocą małych kulek o jednakowych masach. Układ zamocowany jest w punkcie 
i znajduje się w polu ciężkości. W stanie równowagi pręty tworzą kwadrat. Znaleźć częstość małych drgań układu, przy których punkt 
porusza się po linii pionowej.
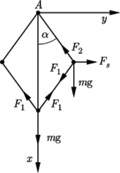
Równania ruchu punktów 
i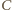 
mają postać: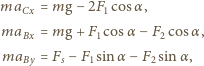
jest masą przegubu, 
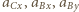są przyspieszeniami punktów 
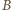i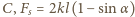 
jest siłą sprężystości. Eliminując z tych równań siły reakcj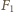i 
i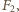 
otrzymujemy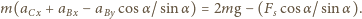
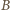i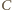 
spełniają związki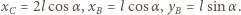
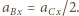Dotychczasowe równania są słuszne dla dowolnego kąta 
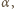ograniczymy teraz nasze rozważania do małych wychyleń z położenia równowagi, gdy 
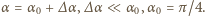Wtedy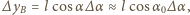 
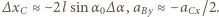W rozważanym przybliżeniu lewa strona równania (1) ma postać 
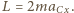W stanie równowagi 
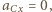stąd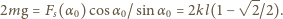
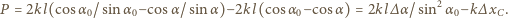
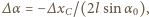otrzymujemy równanie ruchu punktu 
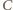dla małych wychyleń z położenia równowagi: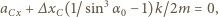
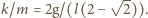Szukana częstość drgań wynosi