Zadanie ZF-813
o zadaniu...
- Publikacja w Delcie: czerwiec 2012
- Publikacja elektroniczna: 02-06-2012
(Hamilton) Cykloida to tor punktu okręgu toczącego się bez poślizgu po prostej. Wykazać, że dowolny pionowy promień oświetlający cykloidę od dołu, odbiwszy się od cykloidy, przechodzi przez punkt, w którym podczas wykreślania cykloidy znajdował się środek tego okręgu.

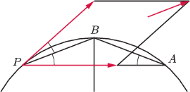
 przechodzi przez najwyższy
punkt wyznaczającego ją okręgu. Istotnie, ponieważ nie ma poślizgu, więc
prędkości ruchu „obrotowego” i postępowego są równej długości,
a ich wypadkowa (czyli wektor styczny) jest dwusieczną kąta między
nimi.
przechodzi przez najwyższy
punkt wyznaczającego ją okręgu. Istotnie, ponieważ nie ma poślizgu, więc
prędkości ruchu „obrotowego” i postępowego są równej długości,
a ich wypadkowa (czyli wektor styczny) jest dwusieczną kąta między
nimi.
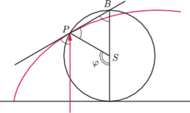
 przecina okrąg w punkcie
przecina okrąg w punkcie
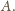 Pionowa średnica okręgu przecina go u góry w punkcie
Pionowa średnica okręgu przecina go u góry w punkcie
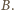 Z symetrii mamy
Z symetrii mamy
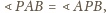 ale kąt
ale kąt
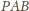 jako
wpisany równy jest kątowi dopisanemu między cięciwą
jako
wpisany równy jest kątowi dopisanemu między cięciwą
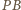 i styczną
do okręgu w
i styczną
do okręgu w
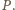 Zatem
Zatem
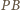 jest dwusieczną kąta między
wektorami.
jest dwusieczną kąta między
wektorami.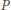 powstały po obrocie okręgu o kąt
powstały po obrocie okręgu o kąt
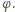 Niech
Niech
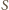 będzie środkiem okręgu. Wówczas
będzie środkiem okręgu. Wówczas
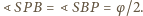 Pionowy
promień jest równoległy do
Pionowy
promień jest równoległy do
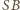 i tworzy ze styczną ten sam kąt co
i tworzy ze styczną ten sam kąt co
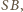 a więc ten sam co
a więc ten sam co
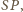 co kończy dowód.
co kończy dowód.