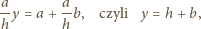Zadanie ZF-814
o zadaniu...
- Publikacja w Delcie: czerwiec 2012
- Publikacja elektroniczna: 02-06-2012
(Huygens) Jaki kształt musi mieć obrotowo symetryczna miseczka, by obiegająca ją poziomo kulka na każdej wysokości poruszała się z tą samą prędkością kątową?

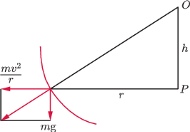
 punkt przecięcia prostej zawierającej tę wypadkową
z osią miseczki i przez
punkt przecięcia prostej zawierającej tę wypadkową
z osią miseczki i przez
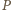 przecięcie tej osi z płaszczyzną ruchu
kulki. Niech
przecięcie tej osi z płaszczyzną ruchu
kulki. Niech
 będzie promieniem zataczanego okręgu i niech
będzie promieniem zataczanego okręgu i niech
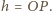
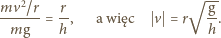
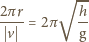
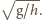 Jedyną zmienną jest tu
Jedyną zmienną jest tu
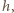 więc
poszukujemy takiej krzywej (będącej przekrojem miseczki), dla której owo
więc
poszukujemy takiej krzywej (będącej przekrojem miseczki), dla której owo
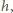 czyli
czyli
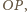 jest stałe.
jest stałe.
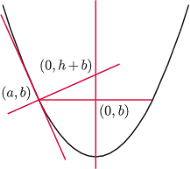
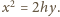 Istotnie, styczna do niej
w punkcie
Istotnie, styczna do niej
w punkcie
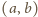 to
to
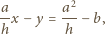
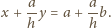
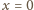 w punkcie
w punkcie